你好,我是黄申。
上一节,我通过问卷调查的案例,给你解释了信息熵和信息增益的概念。被测者们每次回答一道问题,就会被细分到不同的集合,每个细分的集合纯净度就会提高,而熵就会下降。在测试结束的时候,如果所有被测者都被分配到了相应的武侠人物名下,那么每个人物分组都是最纯净的,熵值都为0。于是,测试问卷的过程就转化为“如何将熵从3.32下降到0”的过程。
由于每道问题的区分能力不同,而我们对问题的选择会影响熵下降的幅度。这个幅度就是信息增益。如果问卷题的顺序选择得好,我们可以更快速地完成对用户性格的判定。这一节我们就继续这个话题,看看如何获得一个更简短的问卷设计,把这个核心思想推广到更为普遍的决策树分类算法中。
如何通过信息熵挑选合适的问题?
为了实现一个更简短的问卷,你也许很自然地就想到,每次选择问题的时候,我们可以选择信息增益最高的问题,这样熵值下降得就最快。这的确是个很好的方法。我们来试一试。
我们现在开始选择第一个问题。首先,依次计算“性别”“智商”“情商”“侠义”和“个性”对人物进行划分后的信息增益。我们得到如下结果:

显然,第一步我们会选择“侠义”,之后用户就会被细分为3组。
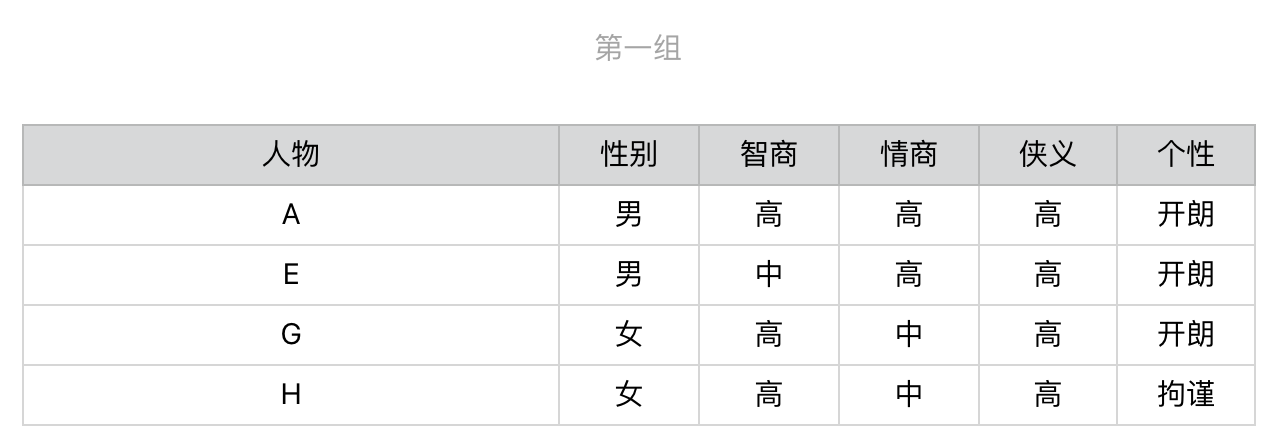
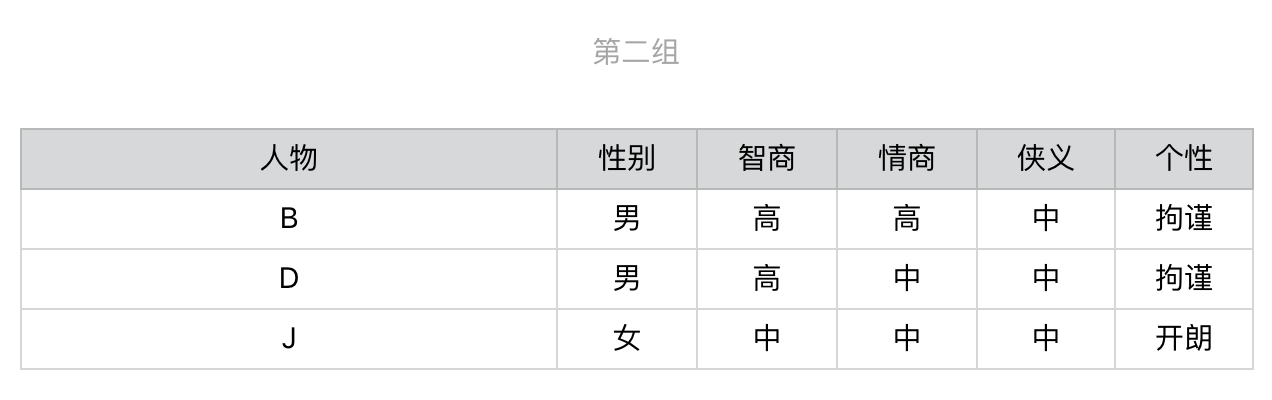
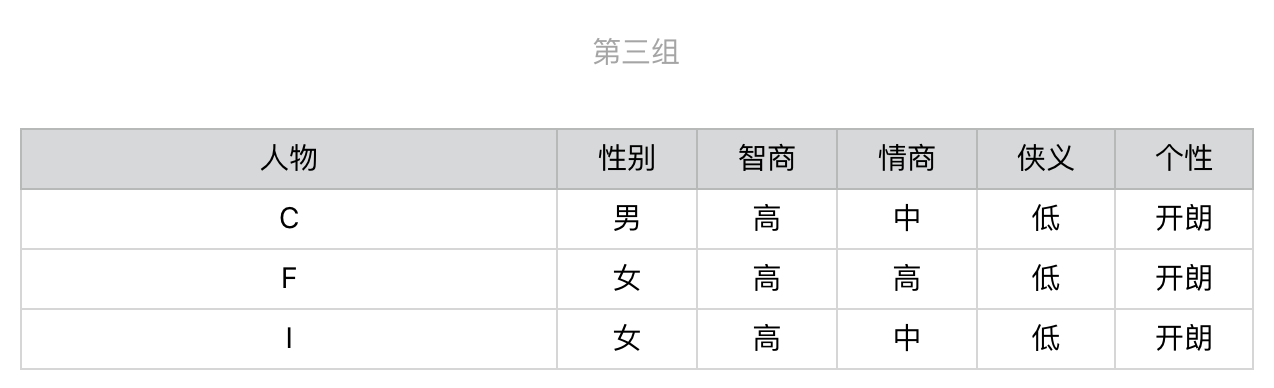
针对第一组,我们继续选择在当前这组中,区分力最强、也是信息增益最高的问题。根据计算的结果我们应该选择有关“性别”的问题,然后进一步地细分。后续的步骤依次类推,直到所有人物都被分开,对于第二组和第三组我们也进行同样地操作。整个过程稍微有点复杂,为了帮你理解,我把它画成了一个图。

从这个图可以看出来,对于每种人物的判断,我们至多需要问3个问题,没有必要问全5个问题。比如,对于人物J和C,我们只需要问2个问题。假设读者属于10种武侠人物的概率是均等的,那么我们就可以利用之前介绍的知识,来计算读者需要回答的问题数量之期望值。每种人物出现的概率是0.1,8种人物需要问3个问题,2种人物需要问2个问题,那么回答问题数的期望值是0.8 * 3 + 0.2 * 2 = 2.8(题)。
如果我们每次不选熵值最高的问题,而选择熵值最低的问题呢?
我计算了一下,最差的情况下,我们要问完全部5个问题,才能确定被测者所对应的武侠人物。而且问4个问题的情况也不少,回答问题数的期望值会在4到5之间,明显要多于基于最高熵来选择题目的方法。当然,如果测试的目标和问题很多,基于熵的问题选择其运算量就会比较大,我们就可以通过编程来自动化整个过程,最终达到优化问卷设计的目的。
好了,现在我们总结一下,如何才能进行高效的问卷调查。最核心的思想是,根据当前的概率分布,挑选在当前阶段区分能力更强的那些问题。具体的步骤有三个。
第一步,根据分组中的人物类型,为每个集合计算信息熵,并通过全部集合的熵值加权平均,获得整个数据集的熵。注意,一开始集合只有一个,并且包含了所有的武侠人物。
第二步,根据信息增益,计算每个问卷题的区分能力。挑选区分能力最强的题目,并对每个集合进行更细的划分。
第三步,有了新的划分之后,回到第一步,重复第一和第二步,直到没有更多的问卷题,或者所有的人物类型都已经被区分开来。这一步也体现了递归的思想。
其实,上述这个过程就体现了训练决策树(Decision Tree)的基本思想。决策树学习属于归纳推理算法之一,适用于分类问题。在前面介绍朴素贝叶斯的时候,我说过,分类算法主要包括了建立模型和分类新数据两个阶段。决定问卷题出现顺序的这个过程,其实就是建立决策树模型的过程。
你可以看到,整个构建出来的图就是一个树状结构,这也是“决策树”这个名字的由来。而根据用户对每个问题的答案,从决策树的根节点走到叶子节点,最后来判断其属于何种人物类型,这个过程就是分类新数据的过程。
让我们把问卷案例泛化一下,将武侠人物的类型变为机器学习中的训练样本,将问卷中的题目变为机器学习中的特征,那么问卷调查的步骤就可以泛化为决策树构建树的步骤。
第一步,根据集合中的样本分类,为每个集合计算信息熵,并通过全部集合的熵值加权平均,获得整个数据集的熵。注意,一开始集合只有一个,并且包含了所有的样本。
第二步,根据信息增益,计算每个特征的区分能力。挑选区分能力最强的特征,并对每个集合进行更细的划分。
第三步,有了新的划分之后,回到第一步,重复第一步和第二步,直到没有更多的特征,或者所有的样本都已经被分好类。
有一点需要注意的是,问卷案例中的每类武侠人物都只有一个样本,而在泛化的机器学习问题中,每个类型对应了多个样本。也就是说,我们可以有很多个郭靖,而且每个人的属性并不完全一致,但是它们的分类都是“郭靖”。正是因为这个原因,决策树通常都只能把整体的熵降低到一个比较低的值,而无法完全降到0。这也意味着,训练得到的决策树模型,常常无法完全准确地划分训练样本,只能求到一个近似的解。
几种决策树算法的异同
随着机器学习的快速发展,人们也提出了不少优化版的决策树。采用信息增益来构建决策树的算法被称为ID3(Iterative Dichotomiser 3,迭代二叉树3代)。但是这个算法有一个缺点,它一般会优先考虑具有较多取值的特征,因为取值多的特征会有相对较大的信息增益。这是为什么呢?
你仔细观察一下信息熵的定义,就能发现背后的原因。更多的取值会把数据样本划分为更多更小的分组,这样熵就会大幅降低,信息增益就会大幅上升。但是这样构建出来的树,很容易导致机器学习中的过拟合现象,不利于决策树对新数据的预测。为了克服这个问题,人们又提出了一个改进版,C4.5算法。
这个算法使用信息增益率(Information Gain Ratio)来替代信息增益,作为选择特征的标准,并降低决策树过拟合的程度。信息增益率通过引入一个被称作分裂信息(Split Information)的项来惩罚取值较多的特征,我把相应的公式给你列出来了。

其中,训练数据集$P$通过属性$T$的属性值,划分为$n$个子数据集,$|Pi|$表示第$i$个子数据集中样本的数量,$|P|$表示划分之前数据集中样本总数量。 这个公式看上去和熵很类似,其实并不相同。
熵计算的时候考虑的是,集合内数据是否属于同一个类,因此即使集合数量很多,但是集合内的数据如果都是来自相同的分类(或分组),那么熵还是会很低。而这里的分裂信息是不同的,它只考虑子集的数量。如果某个特征取值很多,那么相对应的子集数量就越多,最终分裂信息的值就会越大。正是因为如此,人们可以使用分裂信息来惩罚取值很多的特征。具体的计算公式如下:

其中$Gain(P,T)$是数据集$P$使用特征$T$之后的信息增益,$GainRatio(P,T)$是数据集$P$使用特征$T$之后的信息增益率。
另一种常见的决策树是CART算法(Classification and Regression Trees,分类与回归树)。这种算法和ID3、C4.5相比,主要有两处不同:
-
在分类时,CART不再采用信息增益或信息增益率,而是采用基尼指数(Gini)来选择最好的特征并进行数据的划分;
-
在ID3和C4.5决策树中,算法根据特征的属性值划分数据,可能会划分出多个组。而CART算法采用了二叉树,每次把数据切成两份,分别进入左子树、右子树。
当然,CART算法和ID3、C4.5也有类似的地方。首先,CART中每一次迭代都会降低基尼指数,这类似于ID3、C4.5降低信息熵的过程。另外,基尼指数描述的也是纯度,与信息熵的含义相似。我们可以用下面这个公式来计算每个集合的纯度。

其中,$n$为集合$P$中所包含的不同分组(或分类)数量。如果集合$P$中所包含的不同分组越多,那么这个集合的基尼指数越高,纯度越低。
然后,我们需要计算整个数据集的基尼指数。

其中,$m$为全集使用特征$T$划分后,所形成的子集数量。$P_{j}$为第$j$个集合。
无论是何种决策树算法,来自信息论的几个重要概念:信息熵、信息增益、信息增益率、基尼指数都起到了重要的作用。如果你能很好的学习并运用这些概念,那么决策树这种类型的算法就不难理解了。
总结
通过这两节的介绍,我想你对信息熵、信息增益、基尼指数等信息论的概念,以及基于这些概念的决策树分类算法应该有了一定了解。决策树算法的优势在于,容易理解和实现。此外,对于通过样本训练所得的树结构,其每个结点都是基于某个数据特征的判定,对于我们的阅读和解释来说都是很方便的。
当然,决策树也有不足。之前我已经提到,这类算法受训练样本的影响很大,比较容易过拟合。在预测阶段,如果新的数据和原来的训练样本差异较大,那么分类效果就会比较差。为此人们也提出了一些优化方案,比如剪枝和随机森林。如果感兴趣,你可以自己去研究一下。
思考题
刚刚我提到了,如果每次都选择使得信息增益最小的问题,那么构建出来的答题路径就相对冗长。你可以自己动手计算一下用户要回答问题数的期望。
欢迎留言和我分享,也欢迎你在留言区写下今天的学习笔记。如果你有朋友对决策树感兴趣,你可以点击“请朋友读”,把今天的内容分享给他,说不定就帮他解决一个问题。
精选留言
2019-03-05 10:51:18
2019-09-10 06:11:04
信息增益率,计算熵的时候还考虑了多个子项的数目。在计算分组后集合的熵,采用加权平均之后,还要除以,集合分组不同数目引入的熵。
Gini指数是一种新的计算混乱度的方法,熵是基于对数加权的,Gini指数是基于平方的相反数求和再加一。Gini指数求导以后是线性的,随着概率减少变化度比熵更敏感(熵的导数是对数),也就更惩罚小概率事件。
2019-08-07 14:44:21
2019-12-25 08:46:29
2019-09-08 12:37:08
2020-06-21 08:29:21
选择信息增益小的问题对人物分类,问题数的期望值=3.7
选择信息增益大的问题对人物分类,问题数的期望值=2.8
程序代码如下:
import pandas as pd
# 初始化10个武侠人物的属性
p = { '性别':['男','男','男','男','男','女','女','女','女','女']
,'智商':['高','高','高','高','中','高','高','高','高','中']
,'情商':['高','高','中','中','高','高','中','中','中','中']
,'侠义':['高','中','低','中','高','低','高','高','低','中']
,'个性':['开朗','拘谨','开朗','拘谨','开朗','开朗','开朗','拘谨','开朗','开朗']}
name = ['A','B','C','D','E','F','G','H','I','J']
knight = pd.DataFrame(data=p,index=name)
# 定义问题类型及增益大小
problem_type = {'性别':1,'智商':0.72,'情商':0.97,'侠义':1.58,'个性':0.88}
# 计算测试问题的期望值
def get_exp_problems(knight, problem_type):
#BEGIN
result = {}
sub_knight = [(knight,0)]
temp_sub_knight = []
for pt in problem_type:
#用某一个问题类型对每一组侠客进行划分
for sub in sub_knight:
temp_sub = sub[0].groupby(by = [pt])
#该问题没有将该组侠客进行划分,放入中间结果,继续下一组划分
if len(temp_sub) <= 1:
temp_sub_knight.append((sub[0],sub[1]))
continue
# 对划分后的结果进行处理
for label, member in temp_sub:
list_member = list(member.index)
if len(list_member) == 1:
result[list_member[0]] = sub[1] + 1
else:
temp_sub_knight.append((member, sub[1]+1))
sub_knight.clear()
sub_knight.extend(temp_sub_knight)
temp_sub_knight.clear()
# 计算问题数的期望值
exp = 0
for k in result:
exp += result[k]/len(name)
return exp
#END
def main():
problem = dict(sorted(problem_type.items(), key=lambda x: x[1], reverse=False))
print('选择信息增益小的问题对人物分类,问题数的期望值={}'.format(round(get_exp_problems(knight, problem),2)))
problem = dict(sorted(problem_type.items(), key=lambda x: x[1], reverse=True))
print('选择信息增益大的问题对人物分类,问题数的期望值={}'.format(round(get_exp_problems(knight, problem),2)))
if __name__ == '__main__':
main()
2020-04-19 16:28:20
1、思考题:按照最少信息增益来划分,用户回答题目的期望是多少?
0.2*2+0.1*3+0.4*4+0.1*5+0.2*6=4
(换成人话,就是10个人,有两人要回答两题,有一人要回答三题,有四人要回答四题,有一人要回答五题,有两人要回答六题,他们的期望就是四题)
2、关于ID3和C4.5算法:
两者都是罗斯•昆兰(Ross Quinlan)的作品,ID3决策树诞生于1986年,在7年后(1993年)罗斯就推出了它的改进版C4.5算法,后者被称为数据挖掘十大算法之一。
2019-03-10 19:24:41
老师,「基尼指数」没怎么看明白,第一个式子中「n 为集合 P 中所包含的不同分组或分类的数量」该怎么理解?求和符号后面的 pi 是什么含义?谢谢~
2019-02-15 12:40:53
2022-09-05 10:47:15
2020-03-28 13:06:52
2019-11-11 17:34:58
2019-02-21 23:51:22
2020-06-09 12:48:27
我算出来结果是 期望值是3.9。。。跟楼上两个哥们的不一样。。。(因为A、C、D、F、H都要问四轮;B、E、J都要三轮;G、I 要问五轮)不过都是在4的附近
2020-05-18 16:05:00
2020-03-29 21:02:08
2020-02-27 14:24:41
CART算法和 ID3、C4.5 相比,主要有两处不同:
在分类时,CART 不再采用信息增益或信息增益率,而是采用基尼指数(Gini)来选择最好的特征并进行数据的划分;
在 ID3 和 C4.5 决策树中,算法根据特征的属性值划分数据,可能会划分出多个组。
而 CART 算法采用了二叉树,每次把数据切成两份,分别进入左子树、右子树。
2019-08-07 14:20:38
2019-08-07 09:30:23
2019-05-17 11:08:04