和学习小学数学一样,学完了加法之后,我们自然而然就要来学习乘法。既然是退回到小学,我们就把问题搞得简单一点,先来看两个4位数的乘法。这里的4位数,当然还是一个二进制数。我们是人类而不是电路,自然还是用列竖式的方式来进行计算。
十进制中的13乘以9,计算的结果应该是117。我们通过转换成二进制,然后列竖式的办法,来看看整个计算的过程是怎样的。
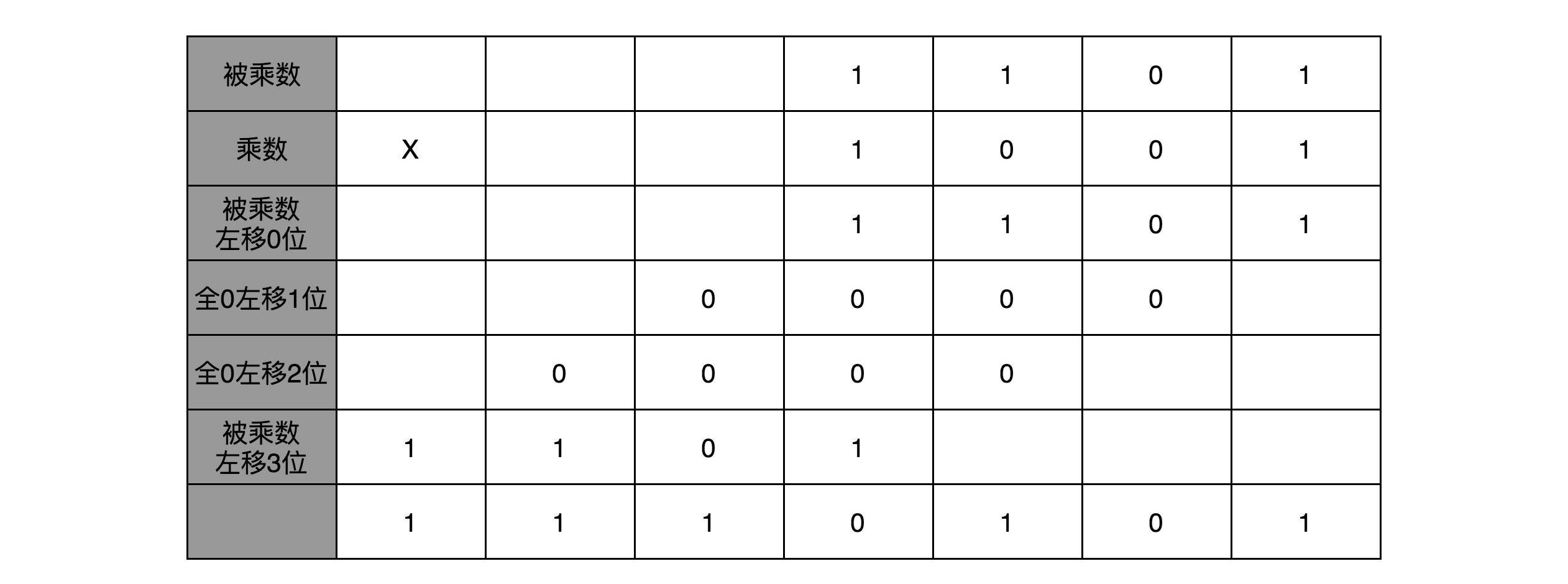
顺序乘法的实现过程
从列出竖式的过程中,你会发现,二进制的乘法有个很大的优点,就是这个过程你不需要背九九乘法口诀表了。因为单个位置上,乘数只能是0或者1,所以实际的乘法,就退化成了位移和加法。
在13×9这个例子里面,被乘数13表示成二进制是1101,乘数9在二进制里面是1001。最右边的个位是1,所以个位乘以被乘数,就是把被乘数1101复制下来。因为二位和四位都是0,所以乘以被乘数都是0,那么保留下来的都是0000。乘数的八位是1,我们仍然需要把被乘数1101复制下来。不过这里和个位位置的单纯复制有一点小小的差别,那就是要把复制好的结果向左侧移三位,然后把四位单独进行乘法加位移的结果,再加起来,我们就得到了最终的计算结果。
对应到我们之前讲的数字电路和ALU,你可以看到,最后一步的加法,我们可以用上一讲的加法器来实现。乘法因为只有“0”和“1”两种情况,所以可以做成输入输出都是4个开关,中间用1个开关,同时来控制这8个开关的方式,这就实现了二进制下的单位的乘法。

至于位移也不麻烦,我们只要不是直接连线,把正对着的开关之间进行接通,而是斜着错开位置去接就好了。如果要左移一位,就错开一位接线;如果要左移两位,就错开两位接线。

这样,你会发现,我们并不需要引入任何新的、更复杂的电路,仍然用最基础的电路,只要用不同的接线方式,就能够实现一个“列竖式”的乘法。而且,因为二进制下,只有0和1,也就是开关的开和闭这两种情况,所以我们的计算机也不需要去“背诵”九九乘法口诀表,不需要单独实现一个更复杂的电路,就能够实现乘法。
为了节约一点开关,也就是晶体管的数量。实际上,像13×9这样两个四位数的乘法,我们不需要把四次单位乘法的结果,用四组独立的开关单独都记录下来,然后再把这四个数加起来。因为这样做,需要很多组开关,如果我们计算一个32位的整数乘法,就要32组开关,太浪费晶体管了。如果我们顺序地来计算,只需要一组开关就好了。
我们先拿乘数最右侧的个位乘以被乘数,然后把结果写入用来存放计算结果的开关里面,然后,把被乘数左移一位,把乘数右移一位,仍然用乘数去乘以被乘数,然后把结果加到刚才的结果上。反复重复这一步骤,直到不能再左移和右移位置。这样,乘数和被乘数就像两列相向而驶的列车,仅仅需要简单的加法器、一个可以左移一位的电路和一个右移一位的电路,就能完成整个乘法。

你看这里画的乘法器硬件结构示意图。这里的控制测试,其实就是通过一个时钟信号,来控制左移、右移以及重新计算乘法和加法的时机。我们还是以计算13×9,也就是二进制的1101×1001来具体看。

这个计算方式虽然节约电路了,但是也有一个很大的缺点,那就是慢。
你应该很容易就能发现,在这个乘法器的实现过程里,我们其实就是把乘法展开,变成了“加法+位移”来实现。我们用的是4位数,所以要进行4组“位移+加法”的操作。而且这4组操作还不能同时进行。因为下一组的加法要依赖上一组的加法后的计算结果,下一组的位移也要依赖上一组的位移的结果。这样,整个算法是“顺序”的,每一组加法或者位移的运算都需要一定的时间。
所以,最终这个乘法的计算速度,其实和我们要计算的数的位数有关。比如,这里的4位,就需要4次加法。而我们的现代CPU常常要用32位或者是64位来表示整数,那么对应就需要32次或者64次加法。比起4位数,要多花上8倍乃至16倍的时间。
换个我们在算法和数据结构中的术语来说就是,这样的一个顺序乘法器硬件进行计算的时间复杂度是 O(N)。这里的N,就是乘法的数里面的位数。
并行加速方法
那么,我们有没有办法,把时间复杂度上降下来呢?研究数据结构和算法的时候,我们总是希望能够把O(N)的时间复杂度,降低到O(logN)。办法还真的有。和软件开发里面改算法一样,在涉及CPU和电路的时候,我们可以改电路。
32位数虽然是32次加法,但是我们可以让很多加法同时进行。回到这一讲开始,我们把位移和乘法的计算结果加到中间结果里的方法,32位整数的乘法,其实就变成了32个整数相加。
前面顺序乘法器硬件的实现办法,就好像体育比赛里面的单败淘汰赛。只有一个擂台会存下最新的计算结果。每一场新的比赛就来一个新的选手,实现一次加法,实现完了剩下的还是原来那个守擂的,直到其余31个选手都上来比过一场。如果一场比赛需要一天,那么一共要比31场,也就是31天。

加速的办法,就是把比赛变成像世界杯足球赛那样的淘汰赛,32个球队捉对厮杀,同时开赛。这样一天一下子就淘汰了16支队,也就是说,32个数两两相加后,你可以得到16个结果。后面的比赛也是一样同时开赛捉对厮杀。只需要5天,也就是O(log2N)的时间,就能得到计算的结果。但是这种方式要求我们得有16个球场。因为在淘汰赛的第一轮,我们需要16场比赛同时进行。对应到我们CPU的硬件上,就是需要更多的晶体管开关,来放下中间计算结果。

电路并行
上面我们说的并行加速的办法,看起来还是有点儿笨。我们回头来做一个抽象的思考。之所以我们的计算会慢,核心原因其实是“顺序”计算,也就是说,要等前面的计算结果完成之后,我们才能得到后面的计算结果。
最典型的例子就是我们上一讲讲的加法器。每一个全加器,都要等待上一个全加器,把对应的进入输入结果算出来,才能算下一位的输出。位数越多,越往高位走,等待前面的步骤就越多,这个等待的时间有个专门的名词,叫作门延迟(Gate Delay)。
每通过一个门电路,我们就要等待门电路的计算结果,就是一层的门电路延迟,我们一般给它取一个“T”作为符号。一个全加器,其实就已经有了3T的延迟(进位需要经过3个门电路)。而4位整数,最高位的计算需要等待前面三个全加器的进位结果,也就是要等9T的延迟。如果是64位整数,那就要变成63×3=189T的延迟。这可不是个小数字啊!
除了门延迟之外,还有一个问题就是时钟频率。在上面的顺序乘法计算里面,如果我们想要用更少的电路,计算的中间结果需要保存在寄存器里面,然后等待下一个时钟周期的到来,控制测试信号才能进行下一次移位和加法,这个延迟比上面的门延迟更可观。
那么,我们有什么办法可以解决这个问题呢?实际上,在我们进行加法的时候,如果相加的两个数是确定的,那高位是否会进位其实也是确定的。对于我们人来说,我们本身去做计算都是顺序执行的,所以要一步一步计算进位。但是,计算机是连结的各种线路。我们不用让计算机模拟人脑的思考方式,来连结线路。
那怎么才能把线路连结得复杂一点,让高位和低位的计算同时出结果呢?怎样才能让高位不需要等待低位的进位结果,而是把低位的所有输入信号都放进来,直接计算出高位的计算结果和进位结果呢?
我们只要把进位部分的电路完全展开就好了。我们的半加器到全加器,再到加法器,都是用最基础的门电路组合而成的。门电路的计算逻辑,可以像我们做数学里面的多项式乘法一样完全展开。在展开之后呢,我们可以把原来需要较少的,但是有较多层前后计算依赖关系的门电路,展开成需要较多的,但是依赖关系更少的门电路。
我在这里画了一个示意图,展示了一下我们加法器。如果我们完全展开电路,高位的进位和计算结果,可以和低位的计算结果同时获得。这个的核心原因是电路是天然并行的,一个输入信号,可以同时传播到所有接通的线路当中。

如果一个4位整数最高位是否进位,展开门电路图,你会发现,我们只需要3T的延迟就可以拿到是否进位的计算结果。而对于64位的整数,也不会增加门延迟,只是从上往下复制这个电路,接入更多的信号而已。看到没?我们通过把电路变复杂,就解决了延迟的问题。
这个优化,本质上是利用了电路天然的并行性。电路只要接通,输入的信号自动传播到了所有接通的线路里面,这其实也是硬件和软件最大的不同。
无论是这里把对应的门电路逻辑进行完全展开以减少门延迟,还是上面的乘法通过并行计算多个位的乘法,都是把我们完成一个计算的电路变复杂了。而电路变复杂了,也就意味着晶体管变多了。
之前很多同学在我们讨论计算机的性能问题的时候,都提到,为什么晶体管的数量增加可以优化计算机的计算性能。实际上,这里的门电路展开和上面的并行计算乘法都是很好的例子。我们通过更多的晶体管,就可以拿到更低的门延迟,以及用更少的时钟周期完成一个计算指令。
总结延伸
讲到这里,相信你已经发现,我们通过之前两讲的ALU和门电路,搭建出来了乘法器。如果愿意的话,我们可以把很多在生活中不得不顺序执行的事情,通过简单地连结一下线路,就变成并行执行了。这是因为,硬件电路有一个很大的特点,那就是信号都是实时传输的。
我们也看到了,通过精巧地设计电路,用较少的门电路和寄存器,就能够计算完成乘法这样相对复杂的运算。是用更少更简单的电路,但是需要更长的门延迟和时钟周期;还是用更复杂的电路,但是更短的门延迟和时钟周期来计算一个复杂的指令,这之间的权衡,其实就是计算机体系结构中RISC和CISC的经典历史路线之争。
推荐阅读
如果还有什么细节你觉得还没有彻底弄明白,我推荐你看一看《计算机组成与设计:硬件/软件接口》的3.3节。
课后思考
这一讲里,我为你讲解了乘法器是怎么实现的。那么,请你想一想,如果我们想要用电路实现一个除法器,应该怎么做呢?需要注意一下,除法器除了要计算除法的商之外,还要计算出对应的余数。
欢迎你在留言区写下你的思考和疑问,和大家一起探讨。你也可以把今天的文章分享给你朋友,和他一起学习和进步。
精选留言
2019-06-02 21:03:23
2019-05-27 16:12:48
空间 vs 时间。
但CPU毕竟也是很珍贵的资源,晶体管也不宜太多,这中间需要相互平衡。
2020-02-25 15:01:54
2019-05-27 14:11:22
这句才是重点,day14 笔记:https://www.cnblogs.com/luoahong/p/10929985.html
2019-05-27 13:03:58
加法器不是由一个与门和一个异或门组成的吗?
2019-06-16 20:25:58
2019-05-27 08:31:42
2021-03-13 09:52:29
2019-08-14 11:59:15
步骤1 从余数寄存器中减去除数寄存器中的值,将结果保存在除数寄存器中;
步骤2 测试余数是否小于0
如果余数小于0,则执行步骤2b;
否则,执行步骤2a;
步骤2a 将商寄存器左移,且最低位设置为1;
步骤2b 将余数寄存器的值跟除数寄存器的值相加,结果存放在余数寄存器中;将商寄存器左移,最低位设置为0;
步骤3 将除数寄存器右移1位
步骤4 测试是否第N+1次执行
如果是,则结束;否则,跳转到步骤1执行;
2021-05-28 17:04:01
2021-04-18 22:22:19
2019-12-18 07:49:52
2019-09-27 23:25:03
2019-09-21 08:54:21
2022-08-04 17:07:12
不言放弃,这次要补回大学欠下的东西。
2021-05-13 15:04:38
2019-07-03 15:27:19
2023-10-28 08:01:47
2、被乘数左移是为了在做加法的时候对齐位次,乘数右移是为了找到下一次要相乘的位。
3、乘法器内部控制测试部件的四个输出信号就有时钟信号和乘数当前需要ALU计算的移出位,一个输入信号应该会包括乘数左移出的位以及结束信号。
2023-02-09 16:29:44
2022-11-03 15:06:37