你好,我是陈东。
当我们在电脑中查找文件的时候,我们一般习惯先打开相应的磁盘,再打开文件夹以及子文件夹,最后找到我们需要的文件。这其实就是一个检索路径。如果把所有的文件展开,这个查找路径其实是一个树状结构,也就是一个非线性结构,而不是一个所有文件平铺排列的线性结构。
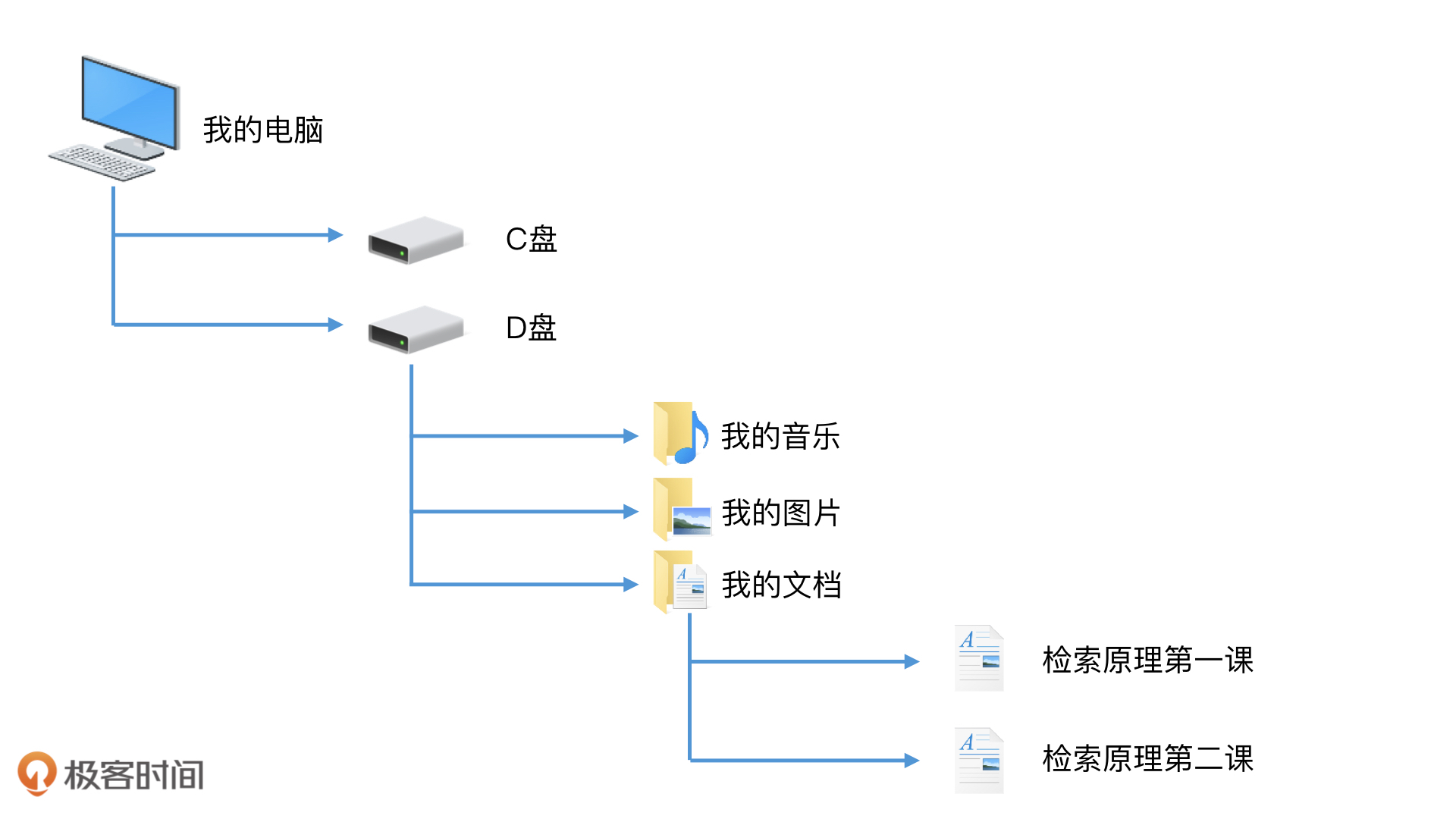
我们都知道,有层次的文件组织肯定比散乱平铺的文件更容易找到。这样熟悉的一个场景,是不是会给你一个启发:对于零散的数据,非线性的树状结构是否可以帮我们提高检索效率呢?
另一方面,我们也知道,在数据频繁更新的场景中,连续存储的有序数组并不是最合适的存储方案。因为数组为了保持有序必须不停地重建和排序,系统检索性能就会急剧下降。但是,非连续存储的有序链表倒是具有高效插入新数据的能力。因此,我们能否结合上面的例子,使用非线性的树状结构来改造有序链表,让链表也具有二分查找的能力呢?今天,我们就来讨论一下这个问题。
树结构是如何进行二分查找的?
上一讲我们讲了,因为链表并不具备“随机访问”的特点,所以二分查找无法生效。当链表想要访问中间的元素时,我们必须从链表头开始,沿着指针一步一步遍历,需要遍历一半的节点才能到达中间节点,时间代价是O(n/2)。而有序数组由于可以“随机访问”,因此只需要O(1)的时间代价就可以访问到中间节点了。
那如果我们能在链表中以O(1)的时间代价快速访问到中间节点,是不是就可以和有序数组一样使用二分查找了?你先想想看该怎么做,然后我们一起来试着改造一下。

既然我们希望能以O(1)的时间代价访问中间节点,那将这个节点直接记录下来是不是就可以了?因此,如果我们把中间节点M拎出来单独记录,那我们的第一步操作就是直接访问这个中间节点,然后判断这个节点和要查找的元素是否相等。如果相等,则返回查询结果。如果节点元素大于要查找的元素,那我们就到左边的部分继续查找;反之,则在右边部分继续查找。
对于左边或者右边的部分,我们可以将它们视为两个独立的子链表,依然沿用这个逻辑。如果想用O(1)的时间代价就能访问这两个子链表的中间节点,我们就应该把左边的中间节点L和右边的中间节点R,单独拎出来记录。
并且,由于我们是在访问完了M节点以后,才决定接下来该去访问左边的L还是右边的R。因此,我们需要将L和M,R和M连接起来。我们可以让M带有两个指针,一个左指针指向L,一个右指针指向R。这样,在访问M以后,一旦发现M不是我们要查找的节点,那么,我们接下来就可以通过指针快速访问到L或者R了。

对于其余的节点,我们也可以进行同样的处理。下面这个结构,你是不是很熟悉?没错,这就是我们常见的二叉树。你可以再观察一下,这个二叉树和普通的二叉树有什么不一样?

没错,这个二叉树是有序的。它的左子树的所有节点的值都小于根节点,同时右子树所有节点的值都大于等于根节点。这样的有序结构,使得它能使用二分查找算法,快速地过滤掉一半的数据。具备了这样特点的二叉树,就是二叉检索树(Binary Search Tree),或者叫二叉排序树(Binary Sorted Tree)。
讲到这里,不知道你有没有发现,尽管有序数组和二叉检索树,在数据结构形态上看起来差异很大,但是在提高检索效率上,它们的核心原理都是一致的。那么,它们是如何提高检索效率的呢?核心原理又一致在哪里呢?接下来,我们就从两个主要方面来看。
- 将数据有序化,并且根据数据存储的特点进行不同的组织。对于连续存储空间的数组而言,由于它具有“随机访问”的特性,因此直接存储即可;对于非连续存储空间的有序链表而言,由于它不具备“随机访问”的特性,因此,需要将它改造为可以快速访问到中间节点的树状结构。
- 在进行检索的时候,它们都是通过二分查找的思想从中间节点开始查起。如果不命中,会快速缩小一半的查询空间。这样不停迭代的查询方式,让检索的时间代价能达到O(log n)这个级别。
说到这里,你可能会问,二叉检索树的检索时间代价一定是O(log n)吗?其实不一定。
二叉检索树的检索空间平衡方案
我们先来看一个例子。假设,一个二叉树的每一个节点的左指针都是空的,右子树的值都大于根节点。那么它满足二叉检索树的特性,是一颗二叉检索树。但是,如果我们把左边的空指针忽略,你会发现它其实就是一个单链表!单链表的检索效率如何呢?其实是O(n),而不是O(log n)。

为什么会出现这样的情况呢?
最根本的原因是,这样的结构造成了检索空间不平衡。在当前节点不满足查询条件的时候,它无法把“一半的数据”过滤掉,而是只能过滤掉当前检索的这个节点。因此无法达到“快速减小查询范围”的目的。
因此,为了提升检索效率,我们应该尽可能地保证二叉检索树的平衡性,让左右子树尽可能差距不要太大。这样无论我们是继续往左边还是右边检索,都可以过滤掉一半左右的数据。
也正是为了解决这个问题,有更多的数据结构被发明了出来。比如:AVL树(平衡二叉树)和红黑树,其实它们本质上都是二叉检索树,但它们都在保证左右子树差距不要太大上做了特殊的处理,保证了检索效率,让二叉检索树可以被广泛地使用。比如,我们常见的C++中的Set和Map等数据结构,底层就是用红黑树实现的。
这里,我就不再详细介绍AVL树和红黑树的具体实现了。为了保证检索效率,我们其实只需要在数据的组织上考虑检索空间的平衡划分就好了,这一点都是一样的。
跳表是如何进行二分查找的?
除了二叉检索树,有序链表还有其他快速访问中间节点的改造方案吗?我们知道,链表之所以访问中间节点的效率低,就是因为每个节点只存储了下一个节点的指针,要沿着这个指针遍历每个后续节点才能到达中间节点。那如果我们在节点上增加一个指针,指向更远的节点,比如说跳过后一个节点,直接指向后面第二个节点,那么沿着这个指针遍历,是不是遍历速度就翻倍了呢?
同理,如果我们能增加更多的指针,提供不同步长的遍历能力,比如一次跳过4个节点,甚至一半的节点,那我们是不是就可以更快速地访问到中间节点了呢?
这当然是可以实现的。我们可以为链表的某些节点增加更多的指针。这些指针都指向不同距离的后续节点。这样一来,链表就具备了更高效的检索能力。这样的数据结构就是跳表(Skip List)。
一个理想的跳表,就是从链表头开始,用多个不同的步长,每隔2^n个节点做一次直接链接(n取值为0,1,2……)。跳表中的每个节点都拥有多个不同步长的指针,我们可以在每个节点里,用一个数组next来记录这些指针。next数组的大小就是这个节点的层数,next[0]就是第0层的步长为1的指针,next[1]就是第1层的步长为2的指针,next[2]就是第2层的步长为4的指针,依此类推。你会发现,不同步长的指针,在链表中的分布是非常均匀的,这使得整个链表具有非常平衡的检索结构。

举个例子,当我们要检索k=a6时,从第一个节点a1开始,用最大步长的指针开始遍历,直接就可以访问到中间节点a5。但是,如果沿着这个最大步长指针继续访问下去,下一个节点是大于k的a9,这说明k在a5和a9之间。那么,我们就在a5和a9之间,用小一个级别的步长继续查询。这时候,a5的下一个元素是a7,a7依然大于k的值,因此,我们会继续在a5和a7之间,用再小一个级别的步长查找,这样就找到a6了。这个过程其实就是二分查找。时间代价是O(log n)。
跳表的检索空间平衡方案
不知道你有没有注意到,我在前面强调了一个词,那就是“理想的跳表”。为什么要叫它“理想”的跳表呢?难道在实际情况下,跳表不是这样实现的吗?的确不是。当我们要在跳表中插入元素时,节点之间的间隔距离就被改变了。如果要保证理想链表的每隔2^n个节点做一次链接的特性,我们就需要重新修改许多节点的后续指针,这会带来很大的开销。
所以,在实际情况下,我们会在检索性能和修改指针代价之间做一个权衡。为了保证检索性能,我们不需要保证跳表是一个“理想”的平衡状态,只需要保证它在大概率上是平衡的就可以了。因此,当新节点插入时,我们不去修改已有的全部指针,而是仅针对新加入的节点为它建立相应的各级别的跳表指针。具体的操作过程,我们一起来看看。
首先,我们需要确认新加入的节点需要具有几层的指针。我们通过随机函数来生成层数,比如说,我们可以写一个函数RandomLevel(),以(1/2)^n的概率决定是否生成第n层。这样,通过简单的随机生成指针层数的方式,我们就可以保证指针的分布,在大概率上是平衡的。
在确认了新节点的层数n以后,接下来,我们需要将新节点和前后的节点连接起来,也就是为每一层的指针建立前后连接关系。其实每一层的指针链接,你都可以看作是一个独立的单链表的修改,因此我们只需要用单链表插入节点的方式完成指针连接即可。
这么说,可能你理解起来不是很直观,接下来,我通过一个具体的例子进一步给你解释一下。
我们要在一个最高有3层指针的跳表中插入一个新元素k,这个跳表的结构如下图所示。

假设我们通过跳表的检索已经确认了,k应该插入到a6和a7两个节点之间。那接下来,我们要先为新节点随机生成一个层数。假设生成的层数为2,那我们就要修改第0层和第1层的指针关系。对于第0层的链表,k需要插入到a6和a7之间,我们只需要修改a6和a7的第0层指针;对于第1层的链表,k需要插入到a5和a7之间,我们只需要修改a5和a7的第1层指针。这样,我们就完成了将k插入到跳表中的动作。
通过这样一种方式,我们可以大大减少修改指针的代价。当然,由于新加入节点的层数是随机生成的,因此在节点数目较少的情况下,如果指针分布的不合理,检索性能依然可能不高。但是当节点数较多的时候,指针会趋向均匀分布,查找空间会比较平衡,检索性能会趋向于理想跳表的检索效率,接近O(log n)。
因此,相比于复杂的平衡二叉检索树,如红黑树,跳表用一种更简单的方式实现了检索空间的平衡。并且,由于跳表保持了链表顺序遍历的能力,在需要遍历功能的场景中,跳表会比红黑树用起来更方便。这也就是为什么,在Redis这样的系统中,我们经常会利用跳表来代替红黑树作为底层的数据结构。
重点回顾
好了,关于非线性结构的检索技术,我们就先讲到这里。我们一起回顾一下今天的重点内容。
首先,对于数据频繁变化的应用场景,有序数组并不是最适合的解决方案。我们一般要考虑采用非连续存储的数据结构来灵活调整。同时,为了提高检索效率,我们还要采取合理的组织方式,让这些非连续存储的数据结构能够使用二分查找算法。
数据组织的方式有两种,一种是二叉检索树。一个平衡的二叉检索树使用二分查找的检索效率是O(log n),但如果我们不做额外的平衡控制的话,二叉检索树的检索性能最差会退化到O(n),也就和单链表一样了。所以,AVL树和红黑树这样平衡性更强的二叉检索树,在实际工作中应用更多。
除了树结构以外,另一种数据组织方式是跳表。跳表也具备二分查找的能力,理想跳表的检索效率是O(log n)。为了保证跳表的检索空间平衡,跳表为每个节点随机生成层级,这样的实现方式比AVL树和红黑树更简单。
无论是二叉检索树还是跳表,它们都是通过将数据进行合理组织,然后尽可能地平衡划分检索空间,使得我们能采用二分查找的思路快速地缩减查找范围,达到O(log n)的检索效率。
除此之外,我们还能发现,当我们从实际问题出发,去思考每个数据结构的特点以及解决方案时,我们就会更好地理解一些高级数据结构和算法的来龙去脉,从而达到更深入地理解和吸收知识的目的。并且,这种思考方式,会在不知不觉中提升你的设计能力以及解决问题的能力。
课堂讨论
今天的内容比较多,你可以结合我留的课堂讨论题,加深理解。
二叉检索树和跳表都能做到O(log n)的查询时间代价,还拥有灵活的调整能力,并且调整代价也是O(log n)(包括了寻找插入位置的时间代价)。而有序数组的查询时间代价也是O(log n),调整代价是O(n),那这是不是意味着二叉检索树或者跳表可以用来替代有序数组呢?有序数组自己的优势又是什么呢?
欢迎在留言区畅所欲言,说出你的思考过程和最终答案。如果有收获,也欢迎把这篇文章分享给你的朋友。
精选留言
2020-03-25 07:34:30
1.有序数据占用的内存空间小于调表
2.有序数组的读取操作能保持在很稳定的时间复杂度,而调表并不能
3.因为数组存储空间是连续的,可以利用内存的局部性原理加快查询
Redis 为何采用跳表而不是红黑树?
1.跳表比红黑树更简单的实现了检索空间的平衡
2.跳表保持了链表顺序遍历的能力,需要遍历的场景,跳表比红黑树用起来方便
2020-03-25 08:53:21
这篇文章让我有很多延伸想法,1,检索操作映射到底层核心就是cpu对存储的寻址方式,而这上层的抽象就是指针和数组,老师向我们展示了添加指针构建二叉树的过程,反过来思考,每个数据项都有对其他数据项的指针,检索问题就变成了留下那些对检索有帮助的指针,可以是比自身大的,可以是和自身相等的。而数组我把它抽象成这样一种结构,即我有一个中心节点知道指向所有数据的指针,而且还知道哪个指针指向的是第几个元素,只不过这里的指针是隐含的。
2 最近一直在想 计算机工程是tradeoff 的艺术,但我感觉大部分人很容易就变成了定性的说这个是时间换空间,这个是低延时是靠降低吞吐来换取的,但这个完全就是纸上的意淫,没有定量的思考就是耍流氓,就好像数组虽然我们说加个元素会导致大量元素迁移,你知道这个迁移的代价是多少吗,就是迁移的数据的个数吗,单位是多少呢? 当然定量又是何其艰难,业务何其复杂,计算机层次又何其多。
2020-03-25 18:39:47
如何确定插入位置?为何使用一个随机的层级?目前还没有头绪…
2020-03-25 07:28:42
2020-03-26 11:33:26
还有一个问题就是对于二叉搜索树而言,如果插入的节点重复了怎么办呢?因为我觉得这个问题虽然在例子中很好解决,如果重复的话,直接放弃插入就是了,但是对于真实的场景又该如何解决呢?希望老师解答。
2020-03-25 17:17:35
2020-04-10 17:51:10
谈谈自身对「高级」的看法。起初总觉得高级就是比数组和链表功能更为强大逻辑更为复杂的数据结构,随着知识的不断学习,发现这种看法虽然不能说是错误的,但也是不全面的。如今我理解的高级觉得其就是基于低级的一种组合。这种组合相当美妙,在仅看外部结构的情况下会觉得像庞然大物难以学习,但找到方法拆解后就会发现其实来去还是老师说的:不外乎数组于链表尔。
好比树这个结构,其本质上就是链表的思想,只是从单指针链表变成了多指针链表,就是最简单的树,然后如果再对其数据排列方式进行限制,就衍生出了更多复杂的树。树本身并不是一个“原子”的数据结构,其实树还能够用数组表示,更为美妙。
再讲高级算法,就想到Java中HashMap的键值对存储实现,为了解决冲突使用链表,后来考虑链表可能出现的严重性能退化,又增加了在一定阈值下转换成红黑树的策略。其实这种内部数据结构的“进化”或“退化”。
包括老师举例的跳表,可以看到,它像链表,但又不是只有单指针,且每个节点的指针数目可能都不一样,而且节点还有层的概念,层又像是数组,那么这样的结构特点究竟有什么好处,这样的数据结构主要用来解决什么问题,为什么要设计成这样才能达到目的。又是老师的灵魂拷问三部曲,思考这些觉得非常有趣。
综上我认为「高级」就是一种表现形式。根据实际的数据场景,数据特点,选择最合适的存储结构,灵活组合或扩展,提供最有效率的存取接口,这算不算是检索的核心呢。
2020-03-25 18:15:05
2020-06-10 12:53:31
2020-03-25 13:39:01
还有就是要考虑业务场景,如果存储的对象本身没有多大,却存了一大堆地址,是得不偿失的。
2020-03-29 19:41:16
2020-03-25 10:41:09
2020-03-25 00:42:09
2020-04-10 13:32:11
2020-03-29 19:05:25
2020-03-28 17:16:26
2020-03-27 12:26:08
2020-03-25 07:27:41
1.有序数据占用的内存空间小于调表
2.有序数组的读取操作能保持在很稳定的时间复杂度,而调表并不能
3.因为数组存储空间是连续的,可以利用内存的局部性原理加快查询
2020-03-25 01:00:40
2023-04-04 19:20:50