你好,我是陈东。欢迎来到专栏的第一节,今天我们主要探讨的是,对于数组和链表这样的线性结构,我们是怎么检索的。希望通过这个探讨的过程,你能深入理解检索到底是什么。
你可以先思考一个问题:什么是检索?从字面上来理解,检索其实就是将我们所需要的信息,从存储数据的地方高效取出的一种技术。所以,检索效率和数据存储的方式是紧密联系的。具体来说,就是不同的存储方式,会导致不同的检索效率。那么,研究数据结构的存储特点对检索效率的影响就很有必要了。
那今天,我们就从数组和链表的存储特点入手,先来看一看它们是如何进行检索的。
数组和链表有哪些存储特点?
数组的特点相信你已经很熟悉了,就是用一块连续的内存空间来存储数据。那如果我申请不到连续的内存空间怎么办?这时候链表就可以派上用场了。链表可以申请不连续的空间,通过一个指针按顺序将这些空间串起来,形成一条链,链表也正是因此得名。不过,严格意义上来说,这个叫单链表。如果没有特别说明,下面我所提到的链表,指的都是只有一个后续指针的单链表。
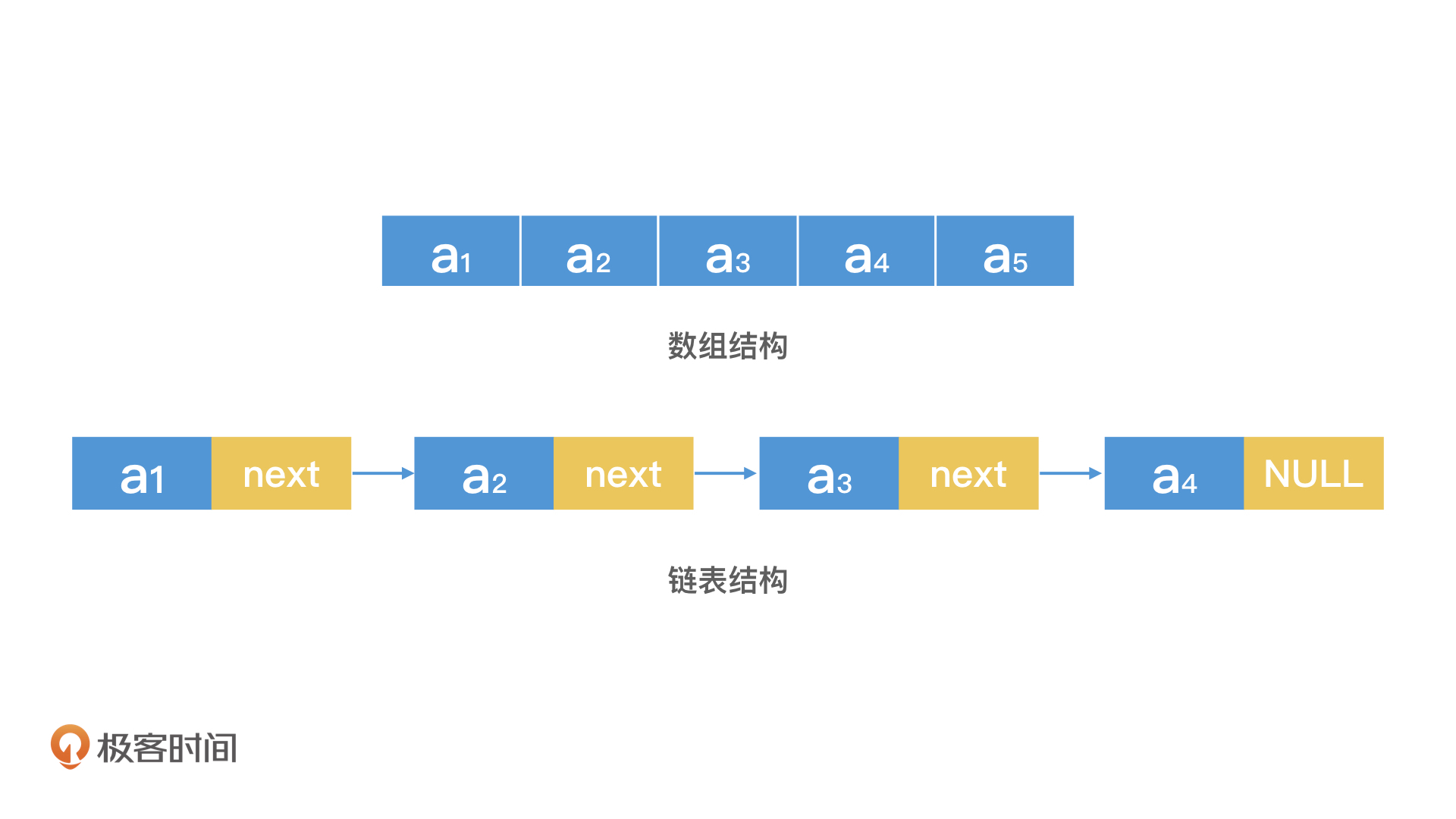
从图片中我们可以看出,数组和链表分别代表了连续空间和不连续空间的最基础的存储方式,它们是线性表(Linear List)的典型代表。其他所有的数据结构,比如栈、队列、二叉树、B+树等,都不外乎是这两者的结合和变化。以栈为例,它本质就是一个限制了读写位置的数组,特点是只允许后进先出。
因此,我们只需要从最基础的数组和链表入手,结合实际应用中遇到的问题去思考解决方案,就能逐步地学习和了解更多的数据结构和检索技术。
那么,数组和链表这两种线性的数据结构的检索效率究竟如何呢?我们来具体看一下。
如何使用二分查找提升数组的检索效率?
首先,如果数据是无序存储的话,无论是数组还是链表,想要查找一个指定元素是否存在,在缺乏数据分布信息的情况下,我们只能从头到尾遍历一遍,才能知道其是否存在。这样的检索效率就是O(n)。当然,如果数据集不大的话,其实直接遍历就可以了。但如果数据集规模较大的话,我们就需要考虑更高效的检索方式。
对于规模较大的数据集,我们往往是先将它通过排序算法转为有序的数据集,然后通过一些检索算法,比如二分查找算法来完成高效的检索。
二分查找也叫折半查找,它的思路很直观,就是将有序数组二分为左右两个部分,通过只在半边进行查找来提升检索效率。那二分查找具体是怎么实现的呢?让我们一起来看看具体的实现步骤。
我们首先会从中间的元素查起,这就会有三种查询结果。
第一种,是中间元素的值等于我们要查询的值。也就是,查到了,那直接返回即可。
如果中间元素的值小于我们想查询的值,那接下来该怎么查呢?这就是第二种情况了。数组是有序的,所以我们以中间元素为分隔,左半边的数组元素一定都小于中间元素,也就是小于我们想查询的值。因此,我们想查询的值只可能存在于右半边的数组中。
对于右半边的数组,我们还是可以继续使用二分查找的思路,再从它的中间查起,重复上面的过程。这样不停地“二分”下去,每次的检索空间都能减少一半,整体的平均查询效率就是O(log n),远远小于遍历整个数组的代价O(n)。
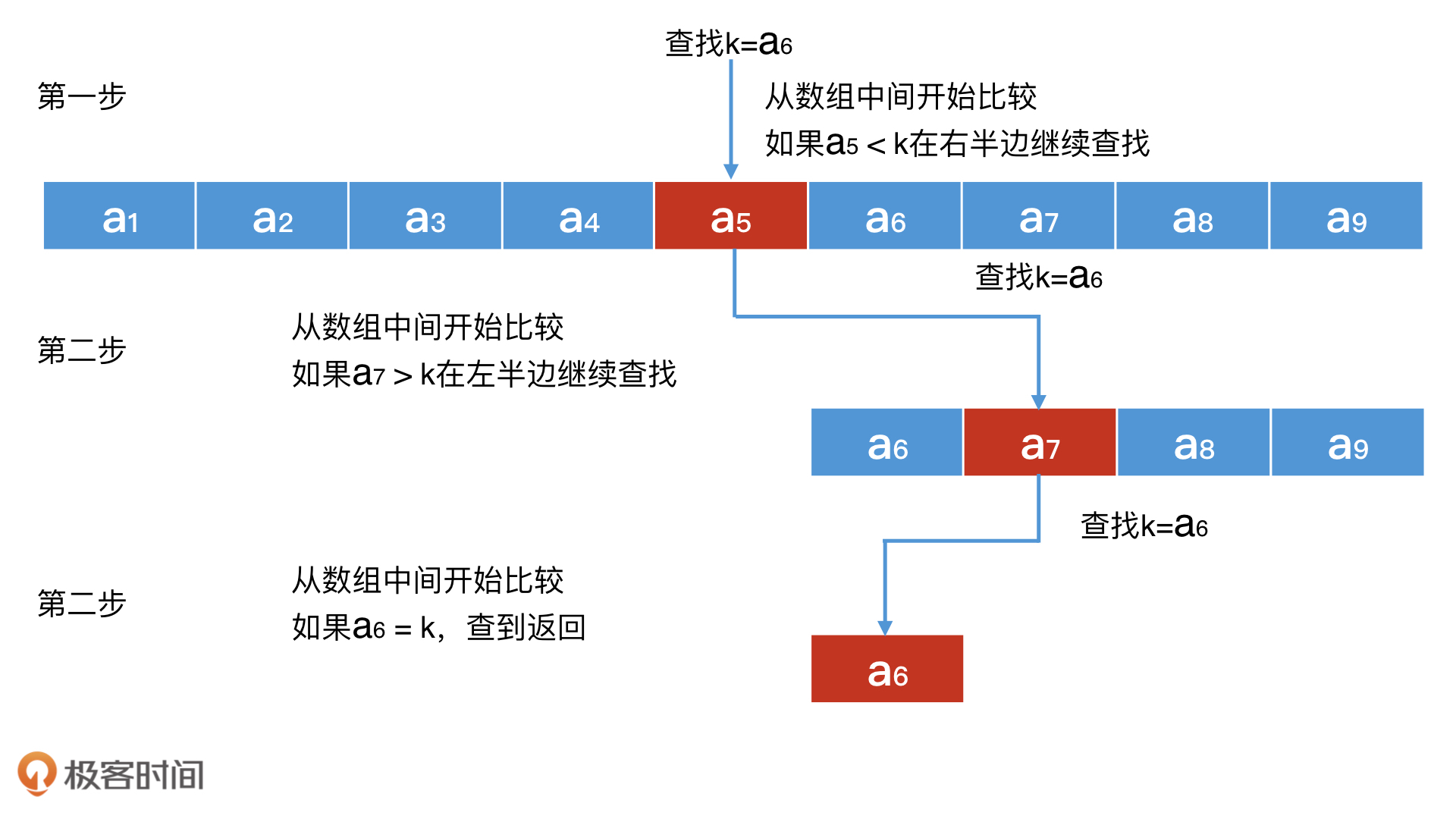
同理,对于第三种情况,如果中间元素的值大于我们想查询的值,那么我们就只在左边的数组元素查找即可。
由此可见,合理地组织数据的存储可以提高检索效率。检索的核心思路,其实就是通过合理组织数据,尽可能地快速减少查询范围。在专栏后面的章节中,我们会看到更多的检索算法和技术,其实它们的本质都是通过灵活应用各种数据结构的特点来组织数据,从而达到快速减少查询范围的目的。
链表在检索和动态调整上的优缺点
前面我们说了,数据无序存储的话,链表的检索效率很低。那你可能要问了,有序的链表好像也没法儿提高检索效率啊,这是为什么呢?你可以先停下来自己思考一下,然后再看我下面的讲解。
数组的“连续空间存储”带来了可随机访问的特点。在有序数组应用二分查找时,它以O(1)的时间代价就可以直接访问到位于中间的数值,然后以中间的数值为分界线,只选择左边或右边继续查找,从而能快速缩小查询范围。
而链表并不具备“随机访问”的特点。当链表想要访问中间的元素时,我们必须从链表头开始,沿着链一步一步遍历过去,才能访问到期望的数值。如果要访问到中间的节点,我们就需要遍历一半的节点,时间代价已经是O(n/2)了。从这个方面来看,由于少了“随机访问位置”的特性,链表的检索能力是偏弱的。
但是,任何事情都有两面性,链表的检索能力偏弱,作为弥补,它在动态调整上会更容易。我们可以以O(1)的时间代价完成节点的插入和删除,这是“连续空间”的数组所难以做到的。毕竟如果我们要在有序的数组中插入一个元素,为了保证“数组有序”,我们就需要将数组中排在这个元素后面的元素,全部顺序后移一位,这其实是一个O(n)的时间代价了。
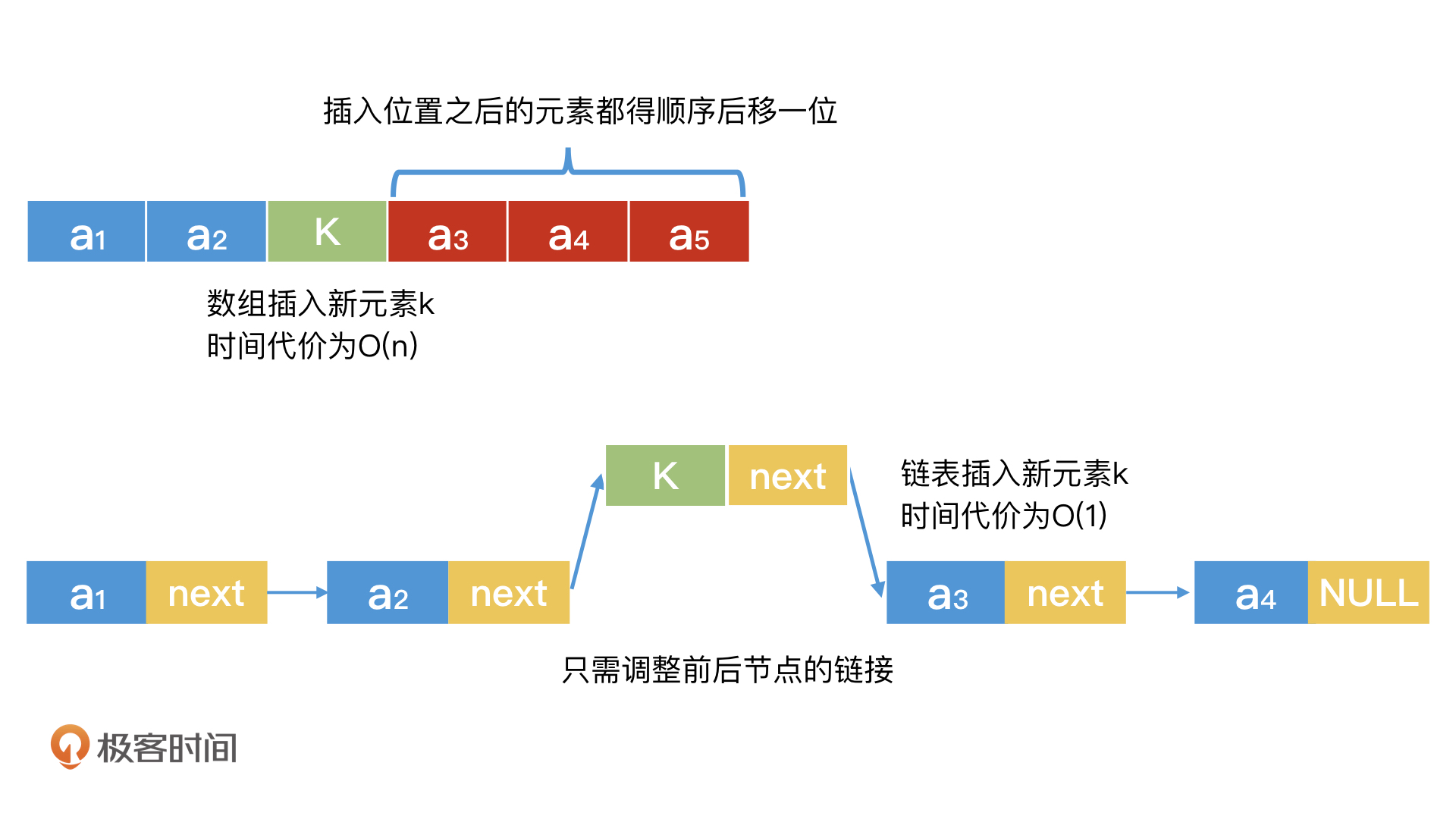
因此,在一些需要频繁插入删除数据的场合,有序数组不见得是最合适的选择。另一方面,在数据量非常大的场合,我们也很难保证能申请到连续空间来构建有序数组。因此,学会合理高效地使用链表,也是非常重要的。
如何灵活改造链表提升检索效率?
本质上,我们学习链表,就是在学习“非连续存储空间”的组织方案。我们知道,对于“非连续空间”,可以用指针将它串联成一个整体。只要掌握了这个思想,我们就可以在不同的应用场景中,设计出适用的数据结构,而不需要拘泥于链表自身的结构限制。
我们可以来看一个简单的改造例子。
比如说,如果我们觉得链表一个节点一个节点遍历太慢,那么我们是不是可以对它做一个简单的改造呢?在掌握了链表的核心思想后,我们很容易就能想到一个改进方案,那就是让链表每个节点不再只是存储一个元素,而是存储一个小的数组。这样我们就能大幅减少节点的数量,从而减少依次遍历节点带来的“低寻址效率”。
比如说,我的链表就只有两个节点,每个节点都存储了一个小的有序数组。这样在检索的时候,我可以用二分查找的思想,先查询第一个节点存储的小数组的末尾元素,看看是否是我们要查询的数字。如果不是,我们要么在第一个节点存储的小数组里,继续二分查找;要么在第二个节点存储的小数组里,继续二分查找。这样的结构就能同时兼顾数组和链表的特点了,而且时间代价也是O(log n)。
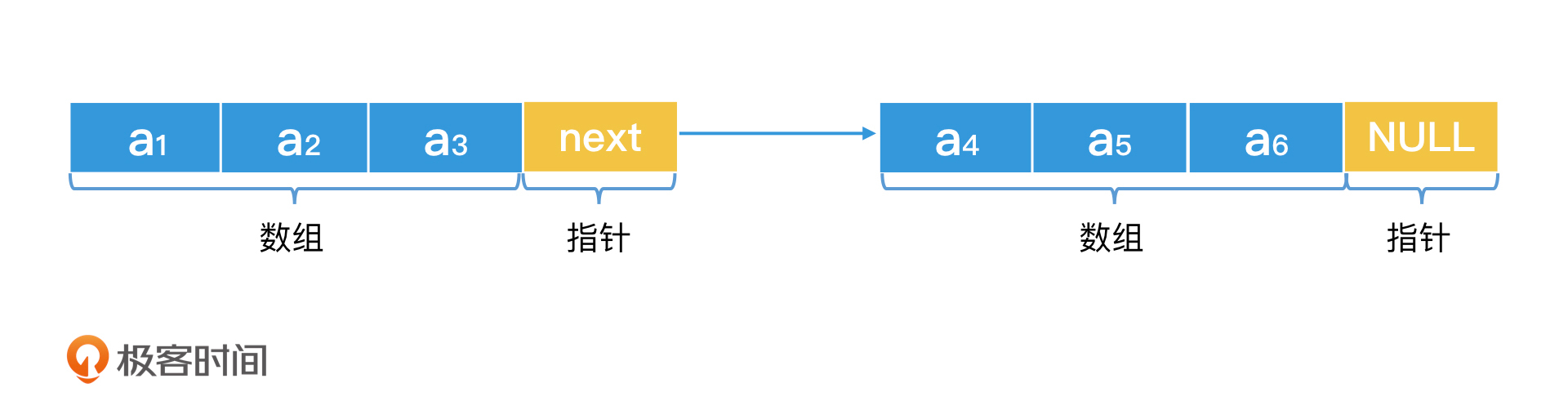
可见,尽管常规的链表只能遍历检索,但是只要我们掌握了“非连续存储空间可以灵活调整”的特性,就可以设计更高效的数据结构和检索算法了。
重点回顾
好了,这一讲的内容差不多了,我们一起回顾一下这一讲的主要内容:以数组和链表为代表的线性结构的检索技术和效率分析。
首先,我们学习了具体的检索方法。对于无序数组,我们可以遍历检索。对于有序数组,我们可以用二分查找。链表具有灵活调整能力,适合用在数据频繁修改的场合。
其次,你应该也开始体会到了检索的一些核心思想:合理组织数据,尽可能快速减少查询范围,可以提升检索效率。
今天的内容其实不难,涉及的核心思想看起来也很简单,但是对于我们掌握检索这门技术非常重要,你一定要好好理解。
随着咱们的课程深入,后面我们会一一解锁更多高级的检索技术和复杂系统,但是核心思路都离不开我们今天所学的内容。
因此,从最基础的数组和链表入手,之后结合具体的问题去思考解决方案,这样可以帮助你一步一步建立起你的知识体系,从而更好地掌握检索原理,达到提高代码效率,提高系统设计能力的目的。
课堂讨论
结合今天学习的数组和链表的检索技术和效率分析,你可以思考一下这两个问题。
- 对于有序数组的高效检索,我们为什么使用二分查找算法,而不是3-7分查找算法,或4-6分查找算法?
- 对于单个查询值k,我们已经熟悉了如何使用二分查找。那给出两个查询值x和y作为查询范围,如果要在有序数组中查找出大于x和小于y之间的所有元素,我们应该怎么做呢?
欢迎在留言区畅所欲言,说出你的思考过程和最终答案。如果有收获,也欢迎把这篇文章分享给你的朋友。
精选留言
2020-03-28 12:33:21
2020-03-23 20:03:29
2020-03-27 00:53:42
二分查找是你在不了解数据分布时的最佳策略,37和46都有靠运气假设的成分
2、
可以先二分从min和max之间找出x,然后再二分从x和max之间找出y,中间的元素就是区间内的
2020-03-24 08:05:44
2.分别用二分查找 x 和 y 对应的下标,然后取中间的数据
2020-03-23 23:37:56
2020-04-14 00:35:41
2020-03-24 21:46:35
2020-03-28 23:09:04
2020-03-25 20:48:58
2020-03-25 07:17:34
2020-03-24 00:28:13
问题2:
1. 二分法查找出x、y;
2. x与y之间的所有元素就是的x到y索引的区间[x索引, y索引]包含的数据。
2020-03-23 18:38:09
2020-04-09 09:55:06
2. 两次二分查找即可
2020-03-28 11:26:15
2020-03-25 12:41:48
2020-03-25 09:29:29
2020-03-24 14:46:52
2020-03-23 19:48:57
对有序数组,先查询最小值的索引,在查询最大值的索引,两者之间的所有值就是这个区间的所有元素
2020-03-23 18:23:36
第二个思考题 先找第一个大于x 然后在找最后一个小于y 这样子就确定了区间。
2023-05-09 22:56:15
1. 对于有序数组的高效检索,我们为什么使用二分查找算法,而不是 3-7 分查找算法,或 4-6 分查找算法?
回答:总体上来看,二分、3-7分、4-6分三种查找算法,均是OK的;都能做到将有序的数组基于规则,不断地缩小判断范围;从而实现O(logn)的检索复杂度;唯一的区别可能就在于二分查找的计算要比3-7分或者4-6分更容易一些;因为是直接除以2的操作,理解上更直观。
2. 对于单个查询值 k,我们已经熟悉了如何使用二分查找。那给出两个查询值 x 和 y 作为查询范围,如果要在有序数组中查找出大于 x 和小于 y 之间的所有元素,我们应该怎么做呢?
回答:第一步利用二分查找计算有序数组中间位置的值,假设为midValue,并与x、y进行比较;如果y <= midValue;则进一步在左半部分的数组中递归继续寻找;同理如果x >= midValue,则在右半部分的数组中递归继续寻找;最终会遇到 x < midValue < y的场景;此时重新划分查询范围,在左半部分继续查找 >x And < midValue的范围值;在右半部分继续查找 > midValue And < y的值;递归查找的过程中可以记录满足体检的元素值,最终形成 > x And < y的所有元素列表。