你好,我是柳博文,欢迎和我一起学习前端工程师的AI实战课。
今天的内容是AI数学知识的选学篇,相信通过数学知识应用篇的学习后,你对AI所需要的数学知识如何应用已经有了不错的理解。
今天这节课,专为想深入学习AI数学知识的前端工程师量身定制,通过一系列精选的数学概念,我们会搭建起通往AI世界的桥梁。我们也将揭示其背后的数学原理,让你在不偏离前端开发舒适区的同时,逐步深化对AI技术的认识。这不仅是一次知识的拓展,更是技能升级的契机,让你在未来能够更加自信地在项目中融入AI元素,推动前端技术与智能科技的融合创新。
现在,就让我们揭开那些支撑AI奇迹的数学面纱,开启你的AI与计算机视觉融合之旅吧。
知识点概览
首先是知识概览。在实践环境,我们用到的技术是目标检测。虽然对于前端来说,日常工作可能不会直接深入到算法实现细节,但了解一些基本的数学知识对于理解算法原理、优化现有库的使用或参与相关项目的开发都是非常有帮助的。
以下是几个关键数学领域的概述,它们与AI目标检测算法紧密相关,你可以参考后面的思维导图。
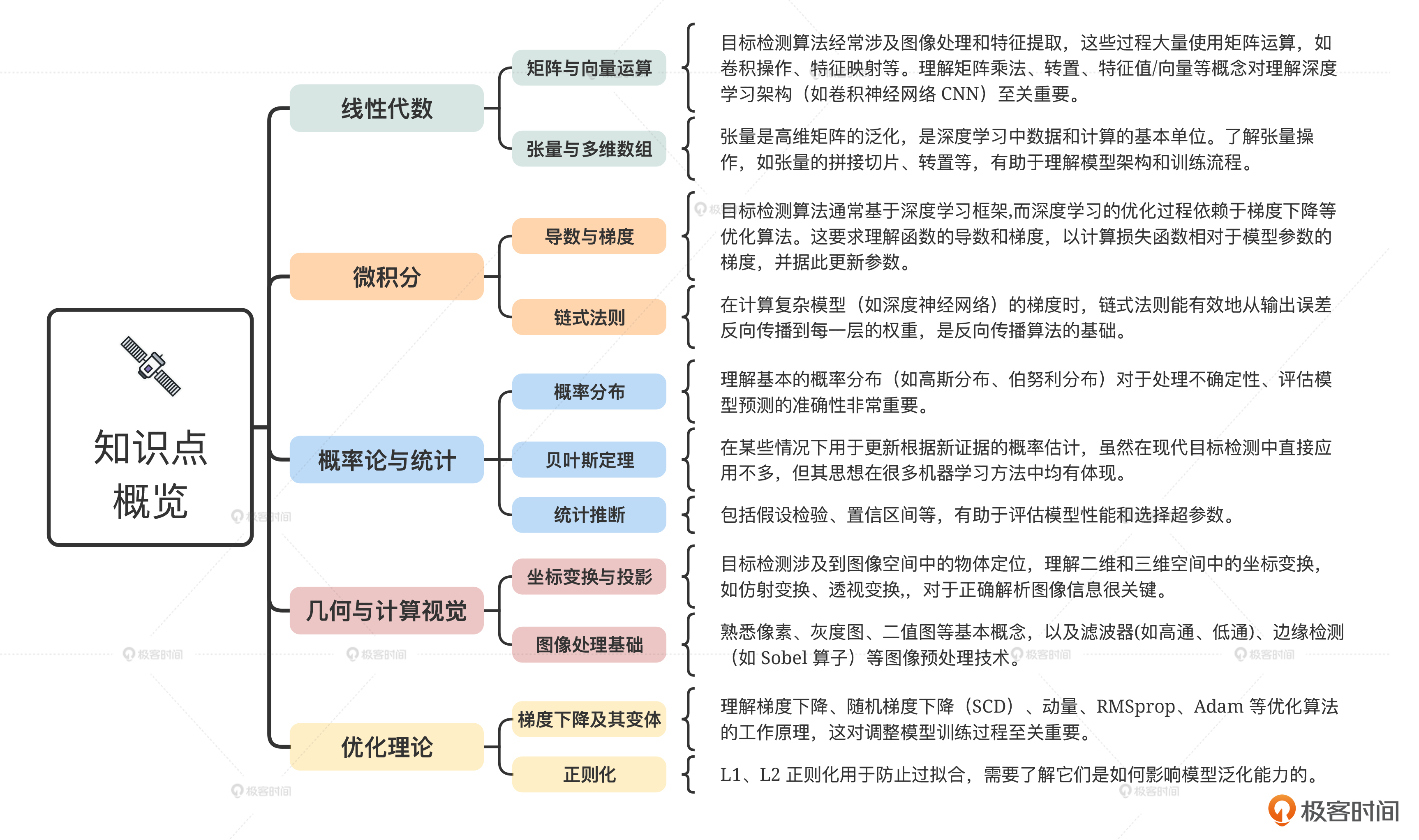
掌握上述数学知识不仅能帮助你深入理解目标检测算法的原理,还能在实践中更加灵活地调整和优化模型。同时,利用现有的库和框架(如TensorFlow.js、PyTorch等),即使不深入所有数学细节,也能快速上手并实现基本的目标检测任务。
科学计算库介绍
现在我们明确了和目标检测紧密相关的知识点都有什么。为了让你更深入地理解它们,最有效的方式就是在本地运行一些简单示例。这时就需要用到一些科学计算库。
在JavaScript领域,有多个科学计算库可供我们选择,来进行数学和矩阵运算,特别适合进行数据处理、统计分析、机器学习等任务。
下面我们就来了解一下三个最为流行的科学计算库,每个库我都提供了一个矩阵乘法的运算实例,你可以通过 npm 安装对应的包,并复制运行代码查看运行结果。
NumJS
NumJS是一个轻量级的JavaScript库,提供了一系列类似MATLAB的数学函数,专为大规模数值计算设计的。它支持多维数组和矩阵运算,适用于浏览器和Node.js环境。
const nj = require('numjs');
let A = nj.array([[1, 2], [3, 4]]);
let B = nj.array([[5, 6], [7, 8]]);
let C = nj.dot(A, B); // 矩阵乘法
console.log(C.tolist()); // 输出矩阵乘法的结果
TensorFlow.js
TensorFlow.js是Google开发的一个JavaScript库,它使开发者能够在浏览器和Node.js中直接运行TensorFlow模型。它不仅支持强大的矩阵和张量运算,还集成了机器学习模型构建、训练和推理功能,非常适合深度学习应用。
import * as tf from '@tensorflow/tfjs';
async function run() {
const a = tf.tensor2d([[1, 2], [3, 4]]);
const b = tf.tensor2d([[5, 6], [7, 8]]);
const c = await a.matMul(b);
c.print(); // 打印矩阵乘法的结果
}
run();
mathJS
mathJS是一个全面的数学库,提供了从基础数学到高级数学的各种功能,包括代数、几何、概率、统计等。它支持多种数据类型,如数字、大数、分数、复数、矩阵等,非常适合进行精确的科学计算。
const math = require('mathjs');
const A = math.matrix([[1, 2], [3, 4]]);
const B = math.matrix([[5, 6], [7, 8]]);
const C = math.multiply(A, B); // 矩阵乘法
console.log(math.format(C)); // 格式化输出矩阵乘法的结果
科学计算库使用小总结
那么这些数据计算库都适合用在什么样的场景里呢?
- NumJS适合需要MATLAB风格API的开发者,侧重于数值计算和小型至中型规模的数据处理项目。
- TensorFlow.js特别适用于深度学习和大型张量运算,适合机器学习项目。
- mathJS提供了最广泛的数学功能,支持多种数据类型,适合需要高度精确和多样化的数学运算场景。
这节课我们选择 mathJS 作为示例实现的库。后面所有示例代码的环境都需要提前安装并导入mathJS包。命令如下:
const math = require('mathjs');
深入细节知识
接下来我们深入知识细节,首先是向量与矩阵的运算。
向量与矩阵及其运算
首先是线性代数中的向量与矩阵,比较重要的分别是向量运算与矩阵运算。
向量
向量是数学中的一个基本概念,尤其在物理学、工程学和计算机科学中应用广泛。向量可以视为既有大小又有方向的数量,通常用箭头表示。在数学上,向量可以看作是一组有序数的集合,称为分量。
向量的基本概念
首先来看向量的定义,一个n维向量v可以表示为(v1, v2, …, vn),其中vi表示向量在第i个维度上的分量。
向量加法
两个n维向量v和w的和v + w是另一个n维向量,其各分量为对应分量之和。
$$v+w=(v1+w1,v2+w2,…,vn+wn)$$
使用mathJS进行实例演示如下:
const v = math.vector([3, 1, 4]);
const w = math.vector([1, 5, 9]);
const sum = math.add(v, w);
console.log(sum); // 输出: [4, 6, 13]
向量减法
向量v减去向量w得到的新向量v - w,其分量为对应分量之差。
$$v−w=(v1−w1,v2−w2,…,vn−wn)$$
使用mathJS进行实例演示如下:
const diff = math.subtract(v, w);
console.log(diff); // 输出: [2, -4, -5]
标量乘法
向量v乘以标量k得到的新向量kv,其各分量为原分量乘以k。
$$kv=(kv1,kv2,…,kvn)$$
const scalar = 2;
const scaledV = math.multiply(scalar, v);
console.log(scaledV); // 输出: [6, 2, 8]
点积(内积)
两个n维向量v和w的点积定义为它们对应分量乘积的和。
$$v⋅w=v1∗w1+v2∗w2+…+vn∗wn$$
const dotProduct = math.dot(v, w);
console.log(dotProduct); // 输出: 32
叉积(外积)
仅限于三维空间中的向量,结果是一个新的向量,其方向垂直于v和w所在平面,大小为v和w构成的平行四边形的面积。
$$\upsilon = (\upsilon1, \upsilon2, \upsilon3), \omega = (\omega1, \omega2, \omega3)$$
$$\upsilon \times \omega = (\upsilon2\omega3 - \upsilon3\omega2, \upsilon3\omega1 - \upsilon1\omega3, \upsilon1\omega2 - \upsilon2\omega1)$$
const dotProduct = math.cross(v, w);
console.log(dotProduct); // 输出: [−11,−23,14]
矩阵
矩阵是数学中一种重要的数据结构,特别是在线性代数中扮演着核心角色。矩阵由行和列组成的数字(或其他数学对象)的矩形排列构成,通常用于表示线性变换、解决线性方程组、表示向量和进行数据分析等。
矩阵的基本概念
定义
一个m×n矩阵是一个由m行n列元素组成的矩形数组,记作A = [aij]m×n,其中aij代表矩阵第i行第j列的元素。
加法与减法
若A和B是同型矩阵(即行数和列数相同),则它们的和C和差D定义为:
$$C=A+B=[cij]=[aij+bij]$$
$$D=A−B=[dij]=[aij−bij]$$
const A = math.matrix([[1, 2], [3, 4]]);
const B = math.matrix([[5, 6], [7, 8]]);
const sum = math.add(A, B);
console.log(sum); // 输出: [[6, 8], [10, 12]]
const diff = math.subtract(A, B);
console.log(diff); // 输出: [[-4, -4], [-4, -4]]
标量乘法
一个矩阵A乘以一个标量k得到的新矩阵,其每个元素都是原矩阵对应元素乘以k。
$$kA=[kaij]$$
const C = math.matrix([[2, 0], [0, 3]]);
const product = math.multiply(A, C);
console.log(product); // 输出: [[2, 6], [6, 12]]
矩阵乘法
如果矩阵A是m×n矩阵,B是n×p矩阵,则它们的乘积C是一个m×p矩阵,其元素cij通过下述公式计算:
$$cij=k=1∑naik⋅bkj$$
矩阵转置
矩阵A的转置AT是一个n×m矩阵,其中元素的行索引与原矩阵的列索引互换,列索引与行索引互换。
$$AT=[aji]$$
const transposeA = math.transpose(A);
console.log(transposeA); // 输出: [[1, 3], [2, 4]]
矩阵的逆
仅当矩阵A是方阵(即m=n)且行列式不为零时,A存在逆矩阵A⁻¹,满足AA⁻¹ = A⁻¹A = I,I为单位矩阵。
const squareMatrix = math.matrix([[4, 1], [2, 3]]);
try {
const inverse = math.inv(squareMatrix);
console.log(inverse); // 输出: [[0.6, -0.2], [-0.4, 0.8]]
} catch (e) {
console.error("The matrix is not invertible.");
}
导数和链式法则
导数理论
导数是微积分中的基本概念之一,表示函数在某一点处的瞬时变化率。如果函数y=f(x)在点x=a处可导,则导数定义为极限形式:
$$f′(a)=\lim_{h \rightarrow 0}{\frac{f(a+h)-f(a)}{h}}$$
导数也可以理解为函数图像在某点处的切线斜率。
链式法则
链式法则是微积分中的一个基本规则,用于计算复合函数的导数。如果y=f(u)且u=g(x),则y=f(g(x))的导数按照链式法则计算为:
$$\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}$$
即外函数对中间变量的导数乘以中间变量对自变量的导数。
使用mathJS计算导数和链式法则
虽然mathJS主要关注于矩阵和向量运算,它也提供了一些基本的微积分功能,但直接计算链式法则的实例可能需要一些间接方法,因为库本身没有直接提供链式法则的函数。不过,我们可以通过计算两个简单函数的导数来展示如何使用mathJS进行微分计算。
计算简单函数的导数
假设要计算函数f(x) = x²的导数。
const f = 'x^2'; // 定义函数表达式
const derivativeF = math.derivative(f, 'x'); // 计算导数,'x'是自变量
console.log(derivativeF.toString()); // 输出: 2*x
间接展示链式法则
虽然直接应用链式法则不易直接通过math.derivative实现,但可以通过手动计算两个步骤来间接展示:
- 计算g(x)=x+1的导数
- 计算f(u)=u²的导数,其中u是g(x)
- 然后根据链式法则手动相乘
const g = 'x + 1';
const derivativeG = math.derivative(g, 'x');
console.log(derivativeG.toString()); // 输出: 1
const fOfU = 'u^2';
const dfDu = math.derivative(fOfU, 'u'); // u代替了原本的x
console.log(dfDu.toString()); // 输出: 2*u
// 按照链式法则手动计算f(g(x))的导数,这里简化展示,实际上`mathJS`没有直接的链式法则应用函数
const chainDerivativeResult = derivativeG * dfDu.substitute('u', g);
console.log(chainDerivativeResult.toString()); // 替换u为g(x)后计算结果
请注意,最后一个步骤展示了如何间接使用mathJS进行链式法则的思想应用,但实际操作中,对于更复杂的函数,可能需要更精细的处理逻辑,或使用其他专门的数学软件或库来直接实现链式法则的计算。
概率论
概率论是研究随机事件发生的可能性的数学分支。它为统计学、机器学习、风险评估等多个领域提供理论基础。概率论中,概率是一个介于0和1之间的数,表示某个事件发生的可能性,其中0表示不可能发生,1表示必然发生。
高斯分布(正态分布)
高斯分布(也称正态分布)是一种连续概率分布,广泛应用于自然界和社会科学中,描述了大量独立同分布变量之和的分布趋势。它由均值(μ)和标准差(σ)决定,图形呈钟形曲线。
$$f(x|\mu,\sigma^{2}) = \frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}}$$
其中,𝑥 是随机变量,𝜇是均值,𝜎2是方差。使用mathJS实现实例如下所示。
// 定义均值(μ)和标准差(σ)
const mean = 0;
const stdDeviation = 1;
// 计算x=1时的高斯分布概率密度函数值
const x = 1;
const gaussianPDF = (x, mean, stdDeviation) => {
const exponent = -(Math.pow(x - mean, 2) / (2 * Math.pow(stdDeviation, 2)));
const denominator = stdDeviation * Math.sqrt(2 * Math.PI);
return Math.pow(Math.E, exponent) / denominator;
};
console.log(`在均值${mean},标准差${stdDeviation}下,x=1的高斯分布概率密度为: ${gaussianPDF(x, mean, stdDeviation).toFixed(4)}`);
伯努利分布
伯努利分布是离散概率分布,用于描述只有两种可能结果的独立实验,通常指成功与失败、是与否等二元结果。它是二项分布的特例,当试验次数n=1时即为伯努利分布。
$$P(X=k∣p)=pk(1−p)1−k$$
其中,𝑋 表示随机变量,取值为0或1;𝑘 是实际观察到的结果(0或1);𝑝 是成功的概率,1−p则是失败的概率。使用mathJS实现实例如下所示。
// 定义成功概率p
const p = 0.7;
// 计算成功(k=1)和失败(k=0)的概率
const successProb = Math.pow(p, 1) * Math.pow(1 - p, 0);
const failureProb = Math.pow(p, 0) * Math.pow(1 - p, 1);
console.log(`成功概率(k=1): ${successProb.toFixed(4)}`);
console.log(`失败概率(k=0): ${failureProb.toFixed(4)}`);
几何视觉
坐标变换与投影
在目标检测中,坐标变换与投影技术用于改变图像中对象的位置、尺寸或视角,以便于识别和分析。这主要包括两类变换。
一类是仿射变换,也就是保持直线性且平行性的变换,包括平移、缩放、旋转和剪切。仿射变换可以用一个3x3的矩阵来表示,其中前两行两列代表线性变换,最后一行为平移向量。
另一类是透视变换,也就是模拟三维空间到二维图像的投影,改变图像的视角。这类变换常用于修正图像的透视失真,或实现图像的鸟瞰图效果。透视变换需要一个3x3的单应性矩阵。
图像处理基础
图像处理是一门十分庞大的学科,这里列举一些我们这门课程会涉及到的点。
-
像素:图像的基本单元,每个像素包含颜色信息,通常用RGB值表示。
-
灰度图:将彩色图像转换为单一亮度值表示,每个像素只有一个强度值。
-
二值图:进一步简化,每个像素非黑即白,常用于边缘检测和形状识别。
-
滤波器:用于图像处理的数学运算。常见的滤波器有两类。高通滤波器可以增强图像的细节,如边缘和噪声,常用于锐化。而低通滤波器可以平滑图像,减少噪声,如均值滤波器。
优化理论
梯度下降理论原理
梯度下降是一种迭代优化算法,主要用于寻找目标函数(如损失函数)最小值的问题。其核心思想是沿着目标函数梯度(函数在某一点的最陡峭方向)的反方向逐步调整参数,直到找到函数值最小的点。
基本步骤:
- 初始化参数:给模型参数一个初始值。
- 计算梯度:对当前参数下的损失函数计算梯度,梯度指向损失函数增大的最快方向。
- 更新参数:按照梯度的负方向,以一定的学习率(步长)调整参数。
- 重复迭代:重复步骤2和3,直到满足停止条件(如梯度接近0,迭代次数达到预设值,或损失函数变化极小)。
批量梯度下降(BGD)与随机梯度下降(SGD)的原理与区别
批量梯度下降(Batch Gradient Descent)
原理:BGD在每次迭代时,会计算整个训练数据集上的损失函数关于模型参数的梯度,然后根据这个梯度更新参数。这意味着每一步更新都是全局最优的方向,但计算成本高,尤其是数据集较大时。
特点:收敛稳定,但计算效率低,不适合大规模数据集。
随机梯度下降(Stochastic Gradient Descent)
原理:SGD在每次迭代时,仅随机选取一个样本来计算梯度并更新参数,因此每一次更新都朝着减小该样本损失的方向。虽然每一步可能不是全局最优方向,但多次迭代后,整体趋向于最小化总体损失。
特点:计算速度快,适合大数据集,但收敛过程可能会更加动荡。
使用mathJS实现BGD与SGD示例
假设我们要最小化一个简单的线性函数的损失:$[ J(\theta) = \frac{1}{2N} \sum_{i=1}^{N} (h_\theta(x_i) - y_i)^2 ]$,其中$hθ(x)=θ0+θ1x$且我们有简单的数据集。
定义数据集、损失函数、梯度计算等函数。
// 简单数据集
const dataset = [
{x: 1, y: 2},
{x: 2, y: 3},
{x: 3, y: 4},
// 更多数据...
];
// 初始化参数
let theta0 = 0;
let theta1 = 0;
const learningRate = 0.01;
const numIterations = 1000;
// 损失函数
function loss(theta0, theta1) {
let totalLoss = 0;
dataset.forEach(data => {
totalLoss += 0.5 * Math.pow((theta0 + theta1 * data.x - data.y), 2);
});
return totalLoss / dataset.length;
}
// 梯度计算
function gradient(theta0, theta1) {
let dTheta0 = 0;
let dTheta1 = 0;
dataset.forEach(data => {
dTheta0 += (theta0 + theta1 * data.x - data.y);
dTheta1 += (theta0 + theta1 * data.x - data.y) * data.x;
});
return {theta0: dTheta0 / dataset.length, theta1: dTheta1 / dataset.length};
}
BGD实现
// 批量梯度下降
for (let i = 0; i < numIterations; i++) {
const gradients = gradient(theta0, theta1);
theta0 -= learningRate * gradients.theta0;
theta1 -= learningRate * gradients.theta1;
// 可以在此打印每轮迭代的损失,观察收敛情况
}
console.log("BGD: theta0 =", theta0, ", theta1 =", theta1);
SGD实现
// 随机梯度下降
for (let i = 0; i < numIterations; i++) {
// 随机选择一个样本
const randomIndex = math.randomInt(0, dataset.length);
const data = dataset[randomIndex];
const gradientSingle = {
theta0: (theta0 + theta1 * data.x - data.y),
theta1: (theta0 + theta1 * data.x - data.y) * data.x
};
theta0 -= learningRate * gradientSingle.theta0;
theta1 -= learningRate * gradientSingle.theta1;
// 同样,可以打印迭代信息
}
console.log("SGD: theta0 =", theta0, ", theta1 =", theta1);
这个示例简化了梯度下降的过程,实际应用中还需考虑更多因素,如学习率调整策略、梯度爆炸或消失的处理等。但对于前端工程师来说,理解这些基本概念和实现过程,有助于深入理解机器学习模型训练背后的数学原理。
总结
这节课对学习AI所需要的基本数学知识做了深入的讲解,现在我们一起做个总结吧。
前端工程师学习目标检测算法,关键在于掌握核心数学概念。理解这些原理,能使工程师更好地运用TensorFlow.js、PyTorch等工具,灵活优化目标检测任务,无需深入全部数学细节。
为了让你更好的理解知识点细节,在对比了多个基于JavaScript的科学计算库以后,我选了mathJS 作为实操演示的工具。mathJS提供了最广泛的数学功能,支持多种数据类型,适合需要高度精确和多样化的数学运算场景。
深入细节知识,向量与矩阵操作是基础(重点要理解向量加减、点积、标量乘及矩阵运算);微积分里面需要掌握导数和链式法则,它们用于优化模型;概率论里主要了解用于评估模型不确定性的高斯、伯努利分布;优化理论中要掌握梯度下降,特别是批量和随机梯度下降,其作用是优化模型训练,使工程师能更高效地应用和调整目标检测技术。
总之,掌握上面这些数学理论知识,能让你更加深入地理解计算机视觉和目标检测,为我们后续的学习打好理论基础。
思考题
请问矩阵运算以及链式求导在模型训练过程中具体作用是什么?
欢迎你在留言区发表你的看法。如果这节课对你有帮助,也推荐你分享给更多的同事、朋友。
精选留言
2025-04-09 15:26:33