你好,我是胡光,欢迎回来。
上节课,我们讲了链表的基础结构,以及体会了一把链表结构在思维逻辑层面的作用,就是面对看似复杂的问题,当我们把它转换成链表结构思维去解决的时候,这些问题和困难都迎刃而解。
今天呢,我将带你学习一种简单、有趣且高效的算法,叫做二分查找。在学习二分查找之前呢,有一个关于二分查找的笑话,你必须知道。
话说,在学校图书馆的计算机科学相关书籍借阅区里面,有一个女生抱着 40 本书往外走,经过图书馆安检机器的时候,安检机器发出了警报声。这时候,女生很无奈,就把书放到了地上,准备一本一本地去试,看看究竟是哪一本书没有消磁。
女生的举动,被旁边图书馆管理员阿姨看到了,阿姨看不下去了,叫住了她,说:这么一本一本的尝试,多慢啊!我教你一种方法。眼看阿姨将书分成两摞,拿起其中一摞的书,过了一下安检,安检机器响了,阿姨就又将这摞书分成了两部分,拿出其中一部分又过了一次安检……就这样,阿姨每次将书的数量减少一半,没几次就找到了那本没有消磁的书。阿姨得意洋洋地说:小姑娘,这就是书中讲的二分查找算法,你这专业知识不过关啊!次日,图书馆发现,丢了 39 本书。
上面这个故事中的阿姨,虽然知道二分查找算法,可明显是对使用算法的前提条件没有搞清楚。今天,我教给你的不仅是二分查找算法本身,还希望你能准确搞清楚二分查找算法的使用场景。
今日任务
在正式开始课程之前呢,先来看一下我们今天这 10 分钟的任务吧。
假设你手上有 n 段长度不等的绳子,你现在想将这些绳子进行裁剪,裁剪出 k 条长度相等的绳子,注意,只能剪断绳子,不能拼接绳子。问题就是,你能得到的这 k 段绳子的最长长度是多长?
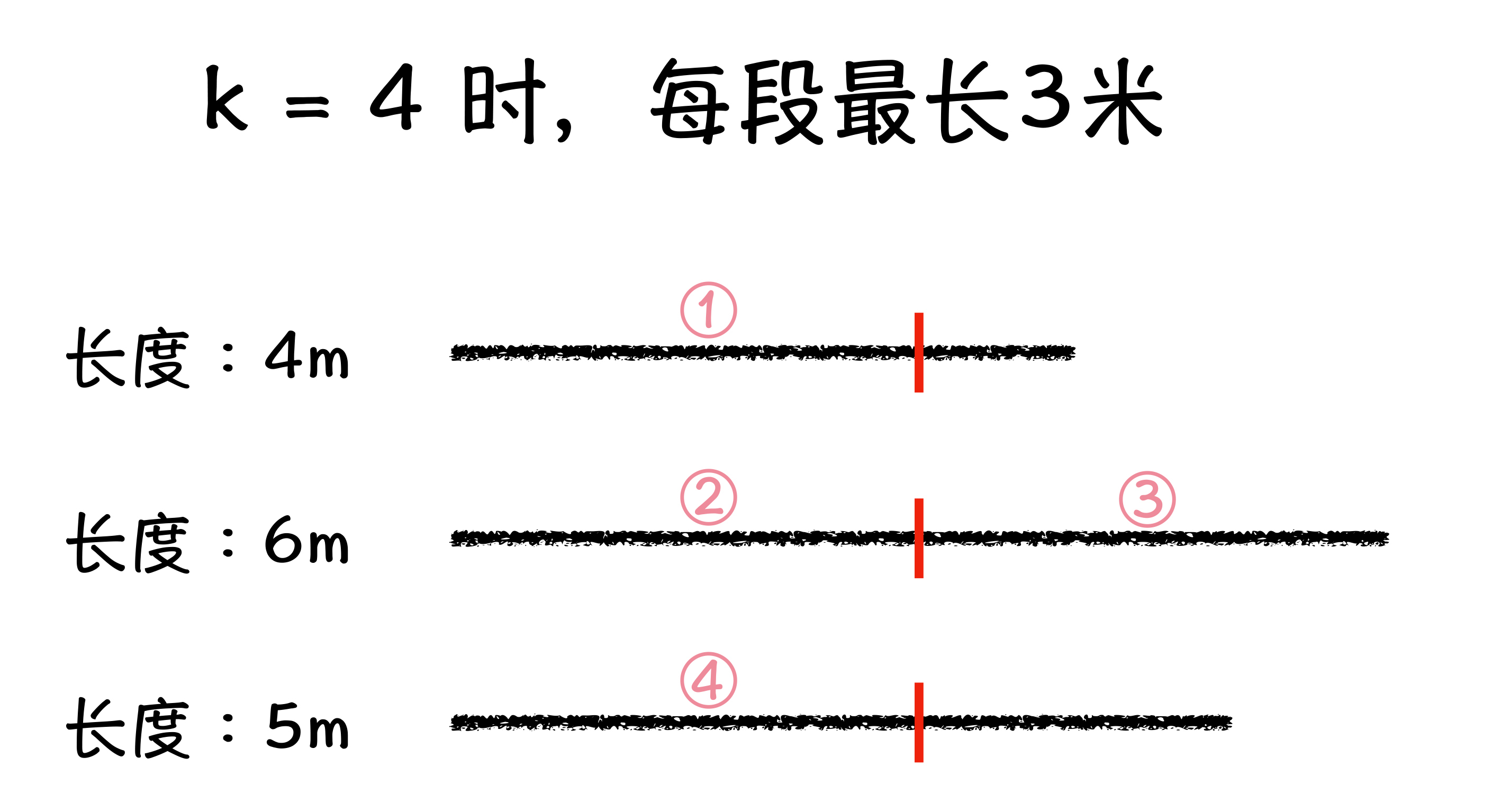
如图所示,如果你手中有 3 条绳子,分别是 4米、6米 和 5米,想要切出等长的4段,你会发现,每段最长就是 3 米。
那么我们是如何得到“每段最长就是3米”这个答案的呢?当然,你可以采用枚举法,就是先尝试能不能切出至少 4 段的 1 米长绳子,如果可以的话,再去尝试每段长度 2 米是否可行,依次尝试下去,直到尝试不下去为止。最后一次尝试可行的长度,就是每段绳子的最长长度了。
这种做法,就像前面故事中想要一本一本进行尝试的女生,显得低效且繁琐。而今天,我将扮演图书馆阿姨的角色,当然,不会像故事中的阿姨一样,犯了前提条件没有搞清的错误,去给你讲一种更高效的方法!
必知必会,查缺补漏
1.二分查找算法基础
最简单的二分算法的形式,就是在一个有序数组中,查找一个数字 x 是否存在。而二分算法,就是要基于这种有序性,才能对原问题进行加速求解。
我们先来思考,如何在一个数组中查找一个数字 x,最直接的方法,就是从头到尾一个一个找,找到了就是有数字x,找不到就是没有数字x。
而二分算法呢,是确定一个查找区间,然后从查找区间的一半处,与 x 进行比较,如果中间的数字比 x 大,说明x 在前半段,就把后半段扔掉;如果比 x 小,就把前半段扔掉,继续在后半段区间内查找。你会发现,二分查找的过程,每一次比较,都会使区间减少一半,对于一个大小为 n 的区间,我们只需要 ${log_2}{n}$ 次比较操作即可确定结果。
具体的过程呢,如下图所示:
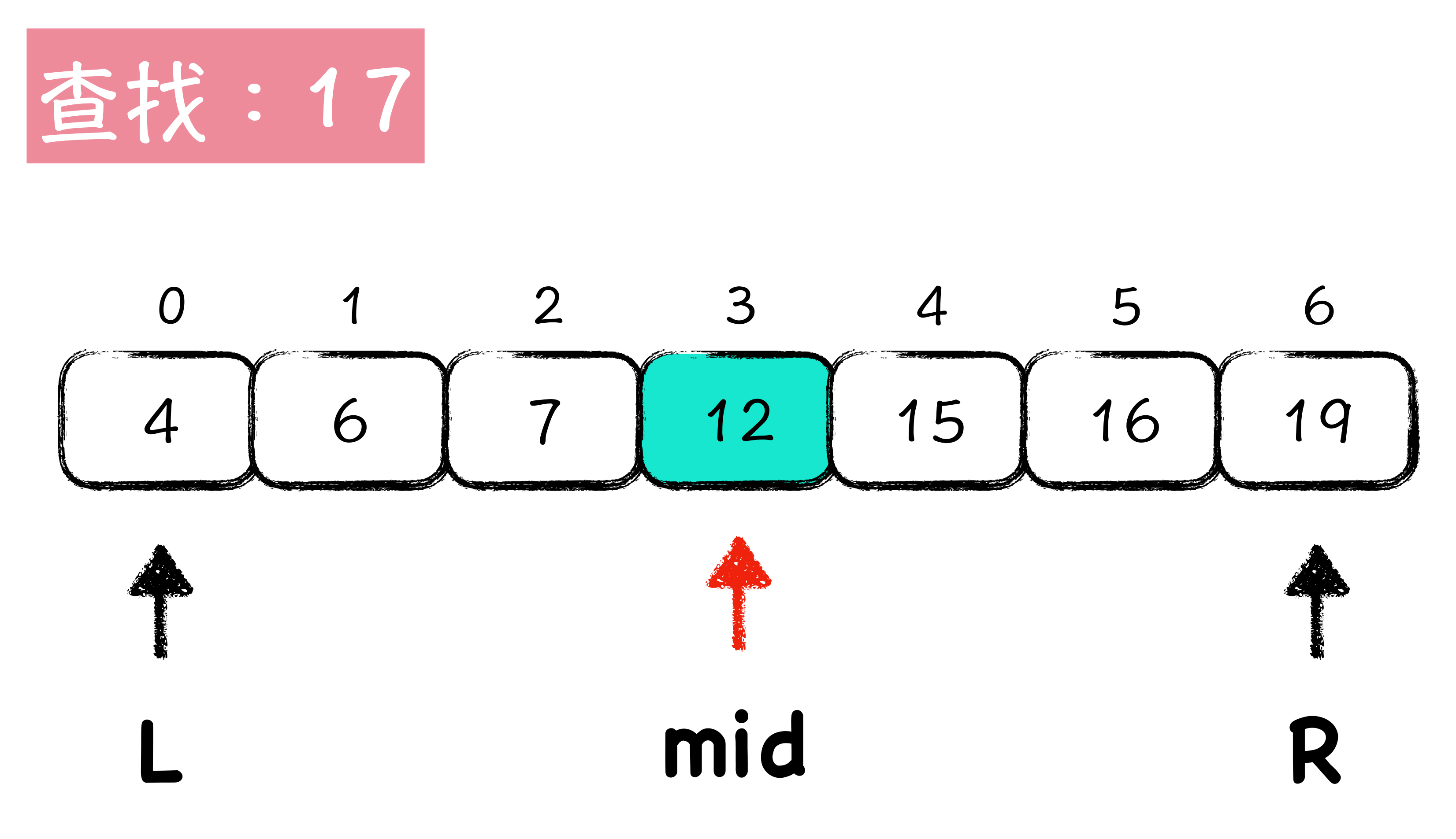
图中呢,我们以查找 17 这个数字为例,L 和 R所圈定的,就是当前的查找区间,一开始 L = 0,R = 6,mid 所指向的就是数组的中间位置,根据 L 和 R 计算得到 mid 的值是 3。查看数组第 3 位的值是 12,比待查找值 17 要小,说明如果 17 在这个有序数组中,那它一定在 mid 所指向位置的后面,而 mid 本身所指向的数字已经确定不是 17 了,所以下一次我们可以将查找区间,定位到 mid + 1 到 R,也就是将 L 调整到 mid + 1 (即数组第4位)的位置。
理解二分查找的过程,首先要理解二分查找是怎么保证查找过程正确性的。中心思想就一个:不管如何调整区间,都要保证待查找数字,总是落在我们的由 L 和 R 标记的查找区间内部。而二分查找,实际上“二分”的就是查找范围。这个过程,就像警察排查犯罪嫌疑人一样,通过一些特定的条件,快速地缩小范围,并锁定真正的罪犯。
下面是一份二分查找的示例代码:
int binary_search(int *arr, int n, int x) {
int l = 0, r = n - 1, mid;
while (l <= r) {
mid = (l + r) >> 1;
if (arr[mid] == x) return mid;
if (arr[mid] > x) r = mid - 1;
else l = mid + 1;
}
return -1;
}
如代码所示,binary_search 函数传入三个参数,分别代表有序数组 arr,数组长度 n 和待查找数字 x。如果在数组中存在数字 x,函数将返回 x 数字的下标,否则就会返回 -1,代表数组中不存在数字 x。
你会看到,函数中有一个 while 循环,循环的执行条件是 l <= r,意味着待查找区间不为空。每次循环开始的时候,都是先通过 l 和 r 的值,计算得到一个中间位置的下标 mid 值,然后比较 mid 位置的值与 x 的大小关系,从而确定区间调整策略。
如果 arr[mid] 大于 x,说明 x 值在区间的前半段,那么mid 及 mid 位置以后的值,就不在下一次查找的范围之内了,我们就把区间的尾部位置 r 向前移动,移动到 mid - 1 位。arr[mid] 小于 x 时候的调整策略与之类似。
至此,我们就讲完了基础的二分查找算法。
2.二分答案的基本思路
其实二分查找的算法思想,最有价值的部分,不是刚才讲的有序数组查找问题。而是由其衍生出来的叫做“二分答案”的思想。
关于二分答案的思想,你可以先回想一下,我们是如何介绍数组与函数的关系的?我们说:数组和函数本质上做的都是映射,函数是压缩的数组,数组是展开的函数。
我们沿着函数和数组的关系,回头再看看二分查找的代码,你会发现二分查找是在一个有序数组中,确定某一位为待查找值的位置,也就是 arr[x] = y,给定待查找 y 值,确定 x 值。对于这个有序数组,我们可以看成是一个单调函数,而对于这个arr[x] = y中去确定 x 值的过程,可以看成是对单调函数 f(x) = y 进行求解的过程。
如何判断,什么场景下需要使用二分思想对问题求解呢?其实,二分能解决的问题,还是比较有代表性的,基本需要满足如下两点:
- f(x) 是一个单调函数。
- f(x) = y 函数,由 x 确定 y 值比较简单,而由 y 值确定 x 就比较困难。
关于第一点,我就不做过多解释了。至于第二点,你可以参考有序数组那个例子,对于数组来说,arr[x] = y,给定数组下标 x,确定值 y,这个过程对于计算机来说很容易,可给定 y 值,确定 y 值所在的下标 x,这个过程就不太容易了。所以,我们使用了二分查找算法。
总地来说,二分答案就是把二分查找过程中的数组换成了函数。关于二分答案的知识,你先理解思想,接下来我会用具体例子来给你展示。
一起动手,搞事情
今天给你留的作业题呢,是一个我们大家普遍都比较关心的问题,与计算工资有关系。下表是“个人所得税缴纳税率表”的一部分:
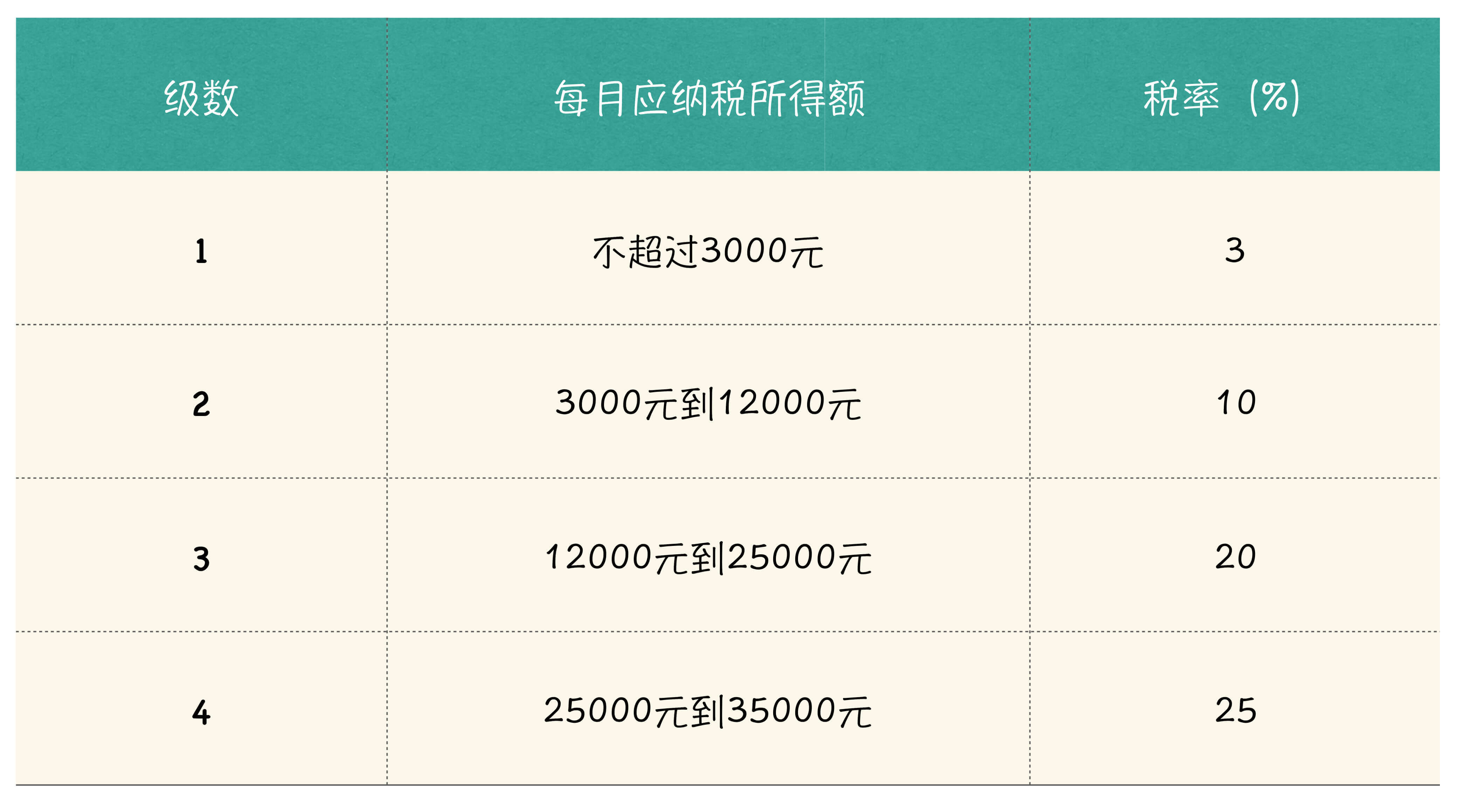
按照表格所示,如果一个人的每月工资是 18600,首先扣除不超过3000部分的3% 的所得税 90 元,然后扣除3000 到 12000 部分的 10%,就是(12000 - 3000) * 10% = 900,最后是扣除 12000 到 18600 的部分的 20%,也就是 (18600 - 12000) * 20% = 1320。所以,此人每月到手工资应该是:18600 - 90 - 900 - 1320 = 16290 元。
如果要是让你通过上表,计算一个人的税后工资,那这个任务可太容易了,我不会将这么简单的任务交给你的。
你今天要做的,是通过一个人的税后工资,反推出他/她的税前工资,也就是针对于上面这个例子,我给出税后工资 16290,你的程序应该能够计算得到税前工资 18600。想一想,怎么做吧,加油!
切出最长的绳子
最后,我们回到今天的任务。我们将每一段绳子的长度 x,与能切出来的绳子段数之间,看成一个映射关系,用函数 f(x) = y 来表示,代表每一段长度为 x 的情况下,最多能切出来 y 段绳子。你很容易发现,f 函数是一个单调函数,随着每一段长度的增加,能切出来的段数 y 是在减少的,而对于我们来说,就是要确定 y = k 时的 x 的最大值。
让我们总结以下 f(x) 函数的性质,首先f(x) 函数是单调函数,x 越大,y 值越小。其次,你应该可以感受出来,当我给你每一段长度 x 的时候,你很容易确定 f(x) = y 的 y 值,而如果让你通过 y 值求解 x,就没那么容易了!
至此,我们从这个任务出现的问题中,看到了能够使用二分思想的两个最重要的性质,下面我们就用二分思想的思路,来解决这个问题,下面是我给出的参考代码:
#define EPS 1e-7
double l[100], n;
int f(double x) {
int cnt = 0;
for (int i = 0; i < n; i++) {
cnt += (int)floor(l[i] / x);
}
return cnt;
}
double binary_search(double *l, double *r, int k) {
if (r - l <= EPS) return r;
double mid = (l + r) / 2.0;
if (f(mid) < k) return bs(l, mid, k);
return bs(mid, r, k);
}
代码中的 binary_search 就是二分答案的过程,函数 f 传入每一段的长度 x,返回最多能切多少段,变量 n 记录的是原始绳子的数量,l 数组记录的是每一段原始绳子的长度。
让我们把目光集中到 binary_search 函数过程,这一段二分答案的程序,使用递归的程序设计技巧,其实和之前给你演示的循环程序本质思想都是一样的。其中 l 和 r 表示待查找区间范围,也就是每一段绳子的长度范围。
递归程序的边界条件,是当 r - l 小于等于一个极小值的时候,就终止递归。这里需要特殊的说明一下,根据浮点数在我们计算机中的表示方法,我们很难用判等操作来判断两个浮点值相等,取而代之的,就是当这两个浮点值已经很接近的时候,我们就认为它俩是一个值。代码中的 EPS 是一个宏,就是我们控制的精度,一般控制在 $10^{-7}$ 范围,两个值相差不到 $10^{-7}$ 的时候,我们就认为这两个浮点值相等。
关于调整搜索范围的代码,我就不再赘述了,剩下的你自己就可以看明白了。至此,我们就解决了今天的任务。
课程小结
最后,我们来做一下课程小结。今天我们学习了二分查找算法,以及由二分思想延伸出来的二分答案相关算法思想。关于这些知识,你只需要记住如下几点即可:
- 二分算法框架,是求解具有单调性问题的利器。
- 二分算法,通常用来求解那些f(x) = y 问题中,给定 y,求解 x 的问题。
- 再次强调,数组和函数在思维层面,没有什么本质差别。
总结完了以后呢,我们再回顾那个笑话故事,图书馆阿姨用二分算法为什么会导致图书馆丢了 39 本书呢?如果我们将书的编号和是否是图书馆的书之间,做一个函数映射的话,你会发现这种映射出来的函数,本质上没有单调性。所以,原因就是阿姨将二分算法思想用错场景了。
好了,今天就到这里了,我是胡光,我们下期见。
精选留言
2020-10-05 16:58:04
课文的例子,完整可运行程序
#include <stdio.h>
#include <math.h>
#define EPS 1e-7
double r[100] = {4, 5, 6}, n;
/*切线段函数*/
int f(double x){
int cnt = 0;
for (int i = 0; i < n; i++){
cnt += (int)floor(r[i] / x);
}
return cnt;
}
/*二分查找函数,可能是环境原因,这里只能的传入变量,而不能像老师那样直接传入数组(指针?)*/
double binary_search(double l, double r, int k){
if(r - l <= EPS)return r;
double mid = (l + r) / 2.0;
if(f(mid) < k) return binary_search(l, mid, k);
return binary_search(mid, r, k);
}
int main(){
n = 3;
double l = 0;
int k = 7;
double b;
for(int i = 0; i < n; i++){
b = binary_search(l, r[i], k);
}
printf("线段最长为%lf", b);
return 0;
}
也许是环境问题,老师的传入数组的BS函数运行不了,我摸索出的方法是二分查找函数里还是传入变量,在主函数里在套一个循环来遍历所有的线段。
2020-10-06 15:11:47
这节课的思考题做起来,感觉像是往4个贴成一排的小盒子里扔一个小球,看这个小球会落在哪一个盒子里。
这里是按要求是使用了二分查找,但我只要知道这个小球在哪个盒子里就行了。
/*思考题 从税后工资反推税前工资,用二分查找法*/
#include <stdio.h>
#include <stdlib.h>
int count = -1;
int ending = -1;
/*范围判断,不讨论税前工资超过35000的情况*/
double test(double y){
if(y > 28910){
puts("你太有钱了,不在讨论范围内。");
exit(0);
}
else return y;
}
/*二分算法,不精确到点,只要知道会落在哪一个区间就好了*/
void binary_search(double x){
double aftertax[5] = {0, 2910, 11010, 21410, 28910};
if(x == aftertax[2])ending = 2;
if(x > aftertax[2]){
if(x < aftertax[3])count = 3;
if(x == aftertax[3])ending = 3;
if(x > aftertax[3])count = 4;
if(x == aftertax[4])count = 4;
}
if(x < aftertax[2]){
if(x < aftertax[1])count = 1;
if(x == aftertax[0])ending = 0;
if(x > aftertax[1])count = 2;
if(x == aftertax[1])ending = 1;
}
}
/*计算函数,从税后工资反推税前工资*/
double f(double y){
double pertax[5] = {0, 3000, 12000, 25000, 35000};
double taxratio[4] = {0.03, 0.1, 0.2, 0.25};
double tax[5] = {0, 90, 900, 2600, 2500};
double x = y;
binary_search(y);
if(ending != -1 && count == -1)printf("\n税前收入是%lf元", pertax[ending]);
if(ending == -1 && count != -1){
for(int i = count; i >= 0; i--){
x += tax[i-1];
}
x -= pertax[count-1] * taxratio[count-1];
x /= (1 - taxratio[count-1]);
printf("\n税前收入是%lf元", x);
}
}
int main(){
puts("税后收入是");
double y = 0;
scanf("%lf", &y);
test(y);
f(y);
return 0;
}
2021-12-08 08:32:12
2021-03-28 00:13:20
#include <stdio.h>
#include <math.h>
#define EPS 1e-7
double arr[100] = {4, 5, 6}, n;
// 切线段函数
int f(double x) {
int cnt = 0;
for (int i = 0; i < n; i++) {
cnt += (int)floor(arr[i] / x);
}
return cnt;
}
double binary_search(double *arr, double l, double r, int k) {
if (r - l <= EPS) {
return r;
}
double mid = (l + r) / 2.0;
if (f(mid) < k) {
return binary_search(arr, l, mid, k);
}
return binary_search(arr, mid, r, k);
}
int main() {
n = 3;
double l = 0, r = 6;
int k = 4;
double res;
res = binary_search(arr, l, r, k);
printf("The longest segment is %lf\n", res);
return 0;
}
2020-10-15 09:53:47
省略计算税后工资的函数double afterTax(double payment);
double beforeTax(double income) {
double l = income / 2;
double r = income * 2;
while (afterTax(l) > income) l /= 2;
while (afterTax(r) < income) r *= 2;
return bsSearch(l, r, income);
}
double bsSearch(double l, double r, double income) {
double mid = (l + r) / 2;
if (afterTax(mid) - income < 1e-7 && income - afterTax(mid) < 1e-7) return mid;
if (afterTax(mid) < income) return bsSearch(mid, r, income);
else return bsSearch(l, mid, income);
}
2020-10-05 16:47:44
最简单的二分查找程序,输入一个数,看在不在数组1-10里,在的话在什么位置。
#include <stdio.h>
/*老师的例子,二分查找函数,输出要么是数组下标,要么不存在(-1)*/
int binary_search(int *arr, int n, int x){
int l = 0, r = n - 1, mid;
while(l <= r){
mid = (l + r) >> 1;
if (arr[mid] == x)return mid;
if (arr[mid] > x)r = mid - 1;
else l = mid + 1;
}
return -1;
}
/*结果宣告函数*/
void yesno(int x){
if(x > 0)printf("yes! is %d", x);
else if(x < 0)puts("no!");
}
int main(){
int arr[10] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int x ;
scanf("%d", &x);
int n = 10;
yesno(binary_search(arr, n, x));
return 0;
}
2020-10-05 16:01:58
老师的例子,这里:double binary_search(double *l, double *r, int k) { if (r - l <= EPS) return r;
我自己跑的时候,返回了[Error] cannot convert 'double*' to 'double' in return
2020-04-16 23:56:49
在题目中求f(x)=y,有限次二分计算中在给定y的情况求解x的问题就是多次取中尝试计算吗?就是经过log2n次计算就可以找到合适的答案……
2020-04-03 13:56:49
```golang
func TestReversePay(t *testing.T) {
taxMatrix := []TaxRange{
TaxRange{Rate: 0.03, Start: 0, End: 3000, QuickValue: 90},
TaxRange{Rate: 0.1, Start: 3000, End: 12000, QuickValue: 900},
TaxRange{Rate: 0.2, Start: 12000, End: 25000, QuickValue: 2600},
TaxRange{Rate: 0.25, Start: 25000, End: 35000, QuickValue: 2500},
}
//1.6 = 1 + 0.03 + 0.1 + 0.2 + 0.25
var coefficient float64 = 1.6
var pays []float64 = []float64{18600, 0.6, 600.6, 8600.6, 10600.6, 106000.15}
for _, pay := range pays {
income := pay - getTax(pay, taxMatrix)
fmt.Println(fmt.Sprintf("income:%f", income))
fmt.Println(fmt.Sprintf("pay:%f", pay))
fmt.Println(fmt.Sprintf("ReversePay:%f", ReversePay(income*coefficient, income, taxMatrix)))
fmt.Println("")
}
}
type TaxRange struct {
Rate float64
Start float64
End float64
QuickValue float64
}
func ReversePay(pay, income float64, taxMatrix []TaxRange) float64 {
guessIncome := pay - getTax(pay, taxMatrix)
if math.Abs(guessIncome-income) <= 1e-7 {
return pay
}
mid := math.Abs(guessIncome-income) / 2
if guessIncome > income {
pay -= mid
} else {
pay += mid
}
return ReversePay(pay, income, taxMatrix)
}
func getTax(pay float64, taxMatrix []TaxRange) float64 {
var tax float64 = 0
for _, taxRange := range taxMatrix {
if pay > taxRange.End {
tax += taxRange.QuickValue
continue
}
tax += (pay - taxRange.Start) * taxRange.Rate
break
}
return tax
}
```
2020-03-09 16:54:26
2020-03-08 18:49:57
//逆函数版本
double f(double x){
if(x <= 3000*0.97) return x/0.97;
if(x <= (3000*0.97 + (12000-3000)*0.9 ))
return ( x- 3000 * 0.97 ) / 0.9 + 3000;
if(x <= (3000*0.97 + (12000-3000)*0.9 + (25000-12000)*0.8 ) )
return ( x- 3000 * 0.97 - (12000-3000)*0.9 ) / 0.8 + 12000 ;
if(x <= (3000*0.97 + (12000-3000)*0.9 + (25000-12000)*0.8 + (35000-25000)*0.75 ) )
return ( x- 3000 * 0.97 - (12000-3000)*0.9 - ( 25000-12000 ) * 0.8 ) / 0.75 + 25000;
else return -1;
}
//二分法版本
#define EPS 1e-7
double ff(double x){
if(x <= 3000) return x*0.97;
if(x <= 12000) return ( x- 3000 ) / 0.9 + 3000*0.97;
if(x <= 25000) return ( x- 12000 ) * 0.8 + 3000 * 0.97 + (12000-3000)*0.9 ;
if(x <= 35000) return ( x- 25000 ) * 0.75 + 3000 * 0.97 + (12000-3000)*0.9 + (25000 - 12000)*0.8;
else return -1;
}
double binary_search(double x, double l , double h ) {
if (h - l <= EPS) return h;
double mid = (h + l) / 2.0;
if(ff(mid) == x) return mid; // 为什么这一行不能换为if(ff(mid) - x <= EPS) return mid;
if (ff(mid) < x) return binary_search(x,mid, h);
return binary_search(x, l, mid);
}
int main(){
double y;
y = f(16290);
printf("%f\n",y);
y = binary_search(16290,0,35000);
printf("%f",y);
}
之前没注意,反函数想错了。 确实二分法 适合(对数时间复杂度) 这种单调函数 二分自变量来寻找目标因变量所对应的自变量的大小。 能避免求逆的繁琐过程出错。
但有个问题,二分法中的这一行代码,必须使用if(ff(mid) == x) return mid;为什么这一行换为if(ff(mid) - x <= EPS) return mid; 会得到错误结果
2020-03-07 23:05:43
double f(double x){
if(x <= 3000*0.97) return x/0.97;
if(x <= (3000*0.97 + (12000-3000)*0.9 ))
return ( x- 3000 * 0.97 ) / 0.9 + 3000*0.97;
if(x <= (3000*0.97 + (12000-3000)*0.9) + (25000-12000)*0.8 )
return ( x- 3000 * 0.97 - (12000-3000)*0.9 ) / 0.8 + 3000*0.97 +(12000-3000)*0.9 ;
if(x <= (3000*0.97 + (12000-3000)*0.9) + (25000-12000)*0.8 + (35000-25000)*0.75 )
return ( x- 3000 * 0.97 - (12000-3000)*0.9 - ( 25000-12000 ) * 0.8 ) / 0.75 + 3000*0.97 +(12000-3000)*0.9 + ( 25000-12000 ) * 0.8;
else return -1;
}
int main(){
double y;
y = f(23534);
printf("%f",y);
}
2020-03-07 08:22:07
2020-03-06 00:11:00
2020-03-04 21:40:03
分段函数关系式,再由每一段 x 的取值范围 得到每一段 y 的取值范围,这样就可以由
已知税后工资与 y 的比较来锁定待求税前工资 x 的取值范围以及对应的函数, 进而
用二分答案法取得待求税前工资的逼近值。 但是,,,没能实现代码,想了很久。
2020-03-03 20:28:09
[0,3000,12000,25000,35000] 然后在按照二分法进行计算