你好,我是胡光,咱们又见面了。
上节课呢,我们讲了大整数表示法的相关知识,并且给你演示了大整数加法及乘法处理过程。其实,你是否掌握了大整数表示法是次要的,主要是你可以在这个过程中,认识到数据结构的作用,也就是我强调的数据结构就是负责表示数据。
原先,我们之所以无法做较大整数的运算,那是因为我们所掌握的数据类型,无法表示很大的数字,有了大整数表示法以后,我们就可以做特别特别大的整数表示了。
我之前也一直在说,算法是做数据计算的,它和数据结构是程序设计中非常重要的两部分。既然是两部分,说明算法和数据结构可以独立分开设计。
关于这点呢,你可以想想上节课我们学的大整数加法,它其实就是算法。为什么这么说呢?你想想,这个加法过程难道是有了大整数以后,才出现的么?显然不是,即使没有大整数表示法,我们还是了解加法过程的,只不过这一次我们用大整数表示法,模拟了加法过程。因此,加法过程是一个独立的算法过程。
总而言之,就是在之前的课程中,我们确定了这样一个结论:如果是计算流程不合理,我们需要改进算法;如果是数据表示受限,我们需要求助于数据结构。
为了让你更清晰地认识到,算法和数据结构是两个可以独立设计的部分,今天我们通过一个具体的算法,来感受一下这个独立设计的过程。
字符串匹配问题
首先让我们来了解一个概念,那就是“字符串匹配问题”。什么意思呢?简单来说,就是在一个大的字符串里面,查找是否包含另外一个较小的字符串。
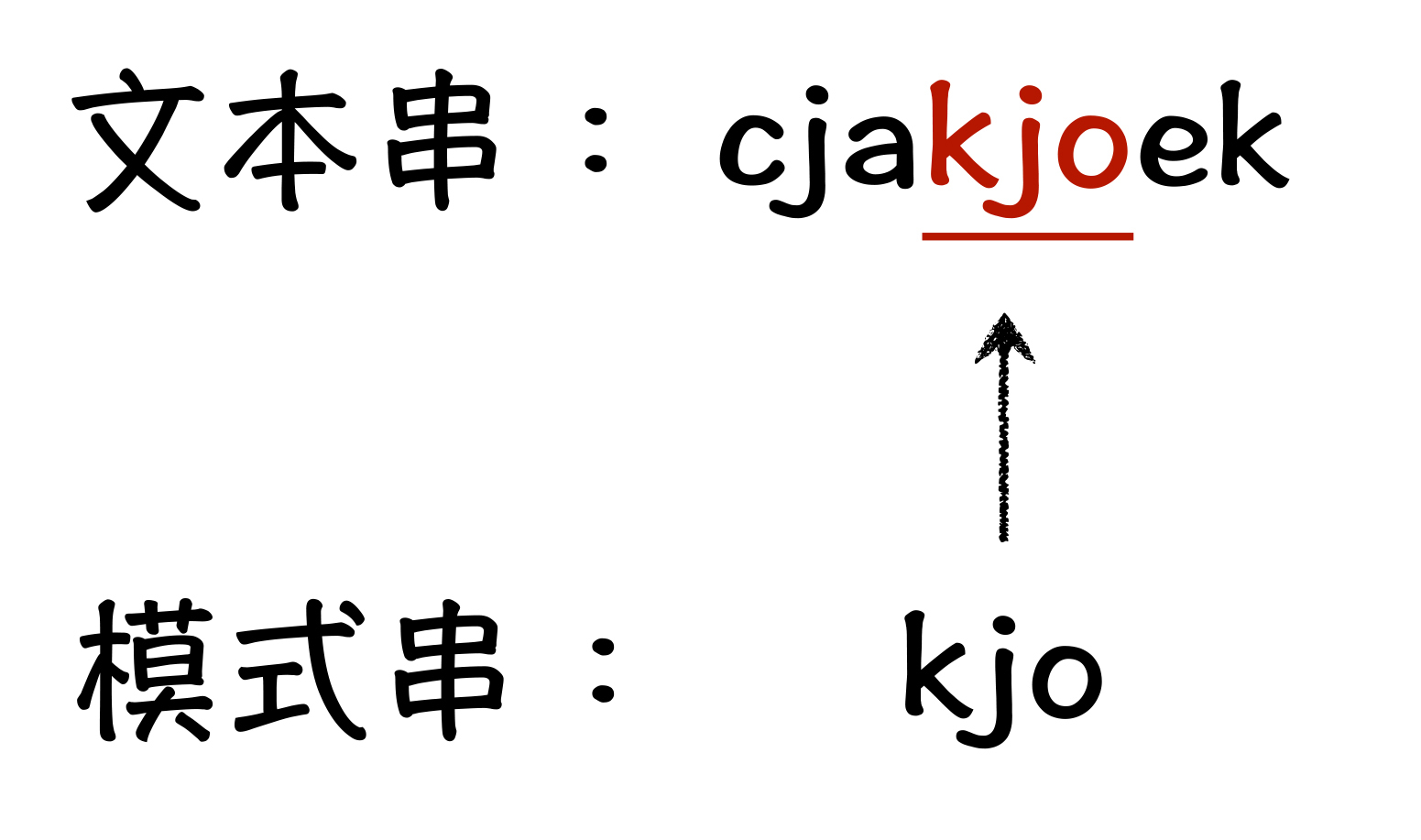
如图所示,我们做的就是在字符串cjakjoek中,查找是否包含字符串kjo,其中,我们把这个cjakjoek字符串叫做文本串,kjo字符串叫做模式串。再举个例子,你手中有一篇英文文档,你想在这个文档中查找所有的 hello 单词。那么,英文文档就是我们所说的文本串,hello 就是模式串。
如果模式串是单独的一个,我们就称这种问题为“单模匹配问题”,如果模式串是多个,那就是“多模匹配问题”。我们今天重点讨论的是“单模匹配问题”。
如果给你一个文本串和模式串,让你查找文本串中是否包含模式串,你用程序怎么完成?最直观的做法,就是用模式串的首字母依次和文本串中的每一位对齐,每次对齐以后,看看所对应区域是否匹配,如果匹配就说明文本串包含模式串。
下面我给出这个方法的程序代码:
// 暴力匹配算法程序
int bruce_force(const char *text, const char *p) {
// 遍历文本串每一位
for (int i = 0; text[i]; i++) {
int flag = 1;
// 从文本串的第 i 位开始与模式串进行匹配
for (int j = 0; p[j]; j++) {
if (text[i + j] == p[j]) continue;
// 当代码到了这里,说明某一位不匹配
flag = 0;
break;
}
if (flag) return 1;
}
return 0;
}
正如你所看到的,这是最简单粗暴的方法。代码中的 bruce_force 程序,就是暴力匹配算法的过程,其中参数 text 就是文本串,p 就是模式串,如果包含模式串,函数返回值是 1,如果不包含,返回值就是 0。
这个程序的效率,可以说是单模匹配的所有算法中最差的了,它的时间复杂度是 O(nm),其中,n 是文本串的长度,m 是模式串的长度。怎么理解呢?就是如果文本串长度是10,模式串长度是 3,那么这个程序差不多要计算30次,外层循环10次,内层循环每次循环 3 次。
按照这个理解,可以设想,当文本串长度是 10000,模式串长度是 1000 的时候,程序的运行次数是接近1000万次这个量级的!所以这种程序的效率最差。
初识 Shift-And 算法
其实,可以高效解决“单模匹配问题” 的算法有很多。今天,我们来学习一种叫做 Shift-And 的算法。
看到 Shift 你会想到什么?是不是电脑键盘上的 Shift 键?我们知道,这个键的作用是做转换,例如当你按住 Shift + 8 的时候,输入的就不是数字 8,而是一个 *。
而 Shift-And 中的另一个单词 And ,其实指代的是位运算中的按位与操作。这两个单词,差不多清晰展示了这个算法的基本流程:首先做信息的转换,然后利用位运算,完成单模匹配问题。下面,我们就来具体对这两步做下讲解。
1. Shift-And 中的信息转换
在 Shift-And 算法中,是将模式串的信息,转换成另外一个种信息格式,如何转换呢?如下图所示:
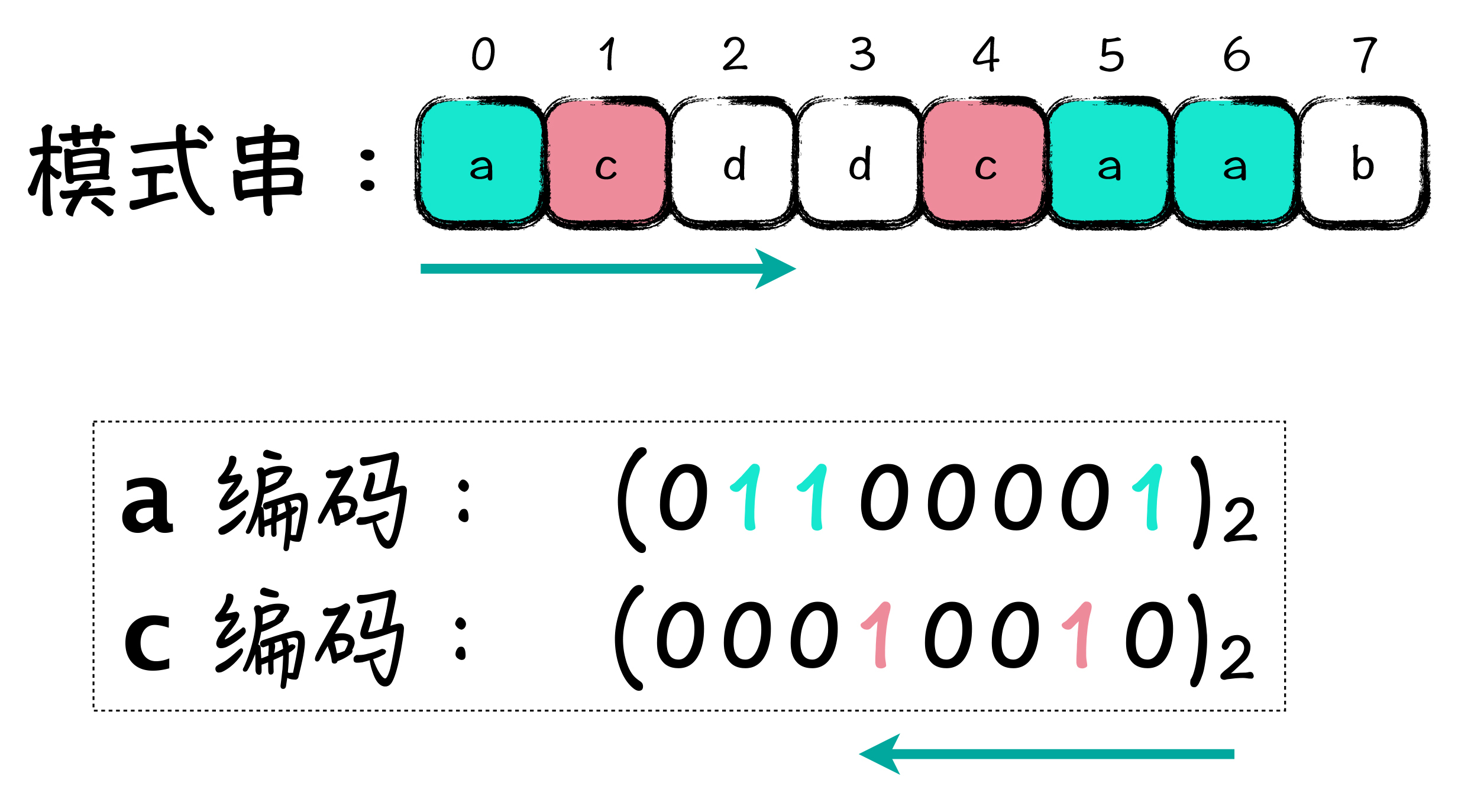
在 Shift-And 中,我们可以把模式串中的每一个字符,转换成一个数字,这个数字一般是由二进制表示。关于转换字符的编码有这么一个规则,就是如果某个字符在模式串的第 i 位中出现过,那么在相关字符编码的二进制数字表示中的第 i 位就为 1。
例如,图中字符 a,在模式串的第 0 位,第 5 位和第 6 位出现过,那么就将 a 字符编码的第 0、5、6 位设置为 1。在这里你需要注意的是,字符数组是从左向右看,也就是说最左边是最低位;而数字是从右向左看的,最右边才是最低位,这里是最容易犯糊涂的地方。
字符 c 呢,由于在第1位和第4位出现过,所以对应到二进制数字中,第1位和第 4 位都是 1,其余位置都是 0。按照这种规则呢,你会发现,没有在模式串中出现的字符,编码值就是 0 值,也就是它的所有二进制位上都是 0。
所以,在 Shift-And 算法中,通过看一个字符的编码,就能知道这个字符,在原模式串的第几位出现过。同时,通过模式串可以生成的编码信息,也可以还原模式串信息。
在之前的课程中,我们讲过类似的概念,一般来说,这种可以相互转换的信息,叫做等价信息表示。说白了就是信息一点儿也没少,只是换了一种表示形式。要想理解 Shift-And 算法,首先就要理解这种等价的信息表示方法。
2.利用位运算做匹配
讲完了信息转换步骤后,我们明确了一个事情,就是 Shift-And 算法中,只是对模式串做了信息转换,但对文本串本质内容没有做任何改动。接下来,我们就来讲解 Shift-And 算法中的 And 部分,也就是来回答 Shift-And 算法,究竟是怎么用位运算来做字符串匹配的。先看下图:
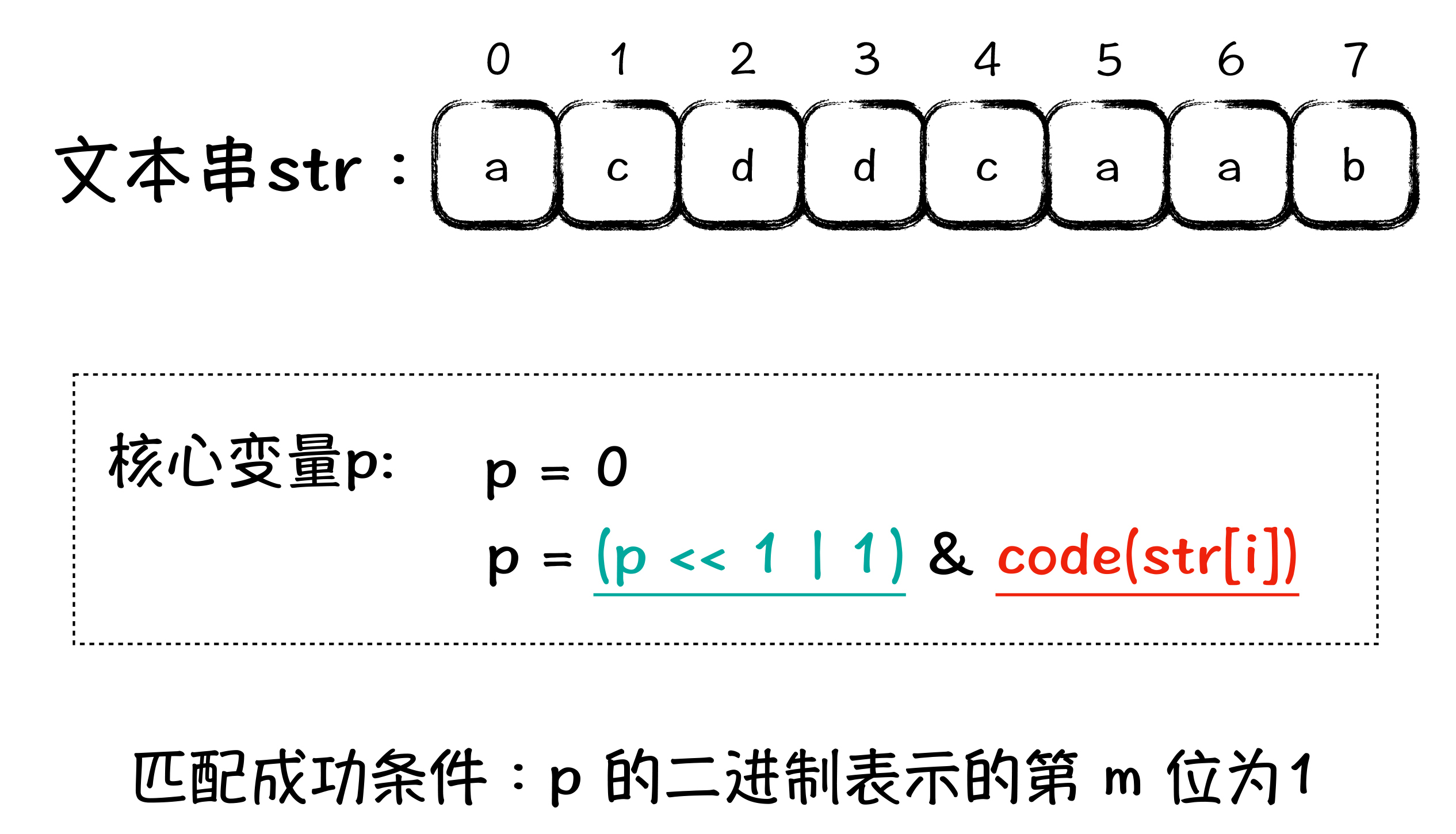
在图中,有一个最关键的,就是 p 变量,它是整个匹配过程的核心变量。我们假设模式串的长度是 m ,code(str[i]) 代表了文本串第 i 位字符的编码,编码方式前面已经介绍过了。整个匹配过程,从前往后,依次处理文本串的每一位,处理到第 i 位的时候,就是用第 i 位字符的编码(code(str[i])),与 p 左移 1 位并或上 1 以后的值(p<< 1 | 1),做“按位与”运算,把得到的值赋给 p 变量。最终,当 p 的二进制表示的第 m 位为 1 时,说明匹配成功了。
为了帮助你理解,我给你准备了一个具体示例,下图是模拟了当模式串为 cdd,文本串为 acdd 时候的匹配流程:
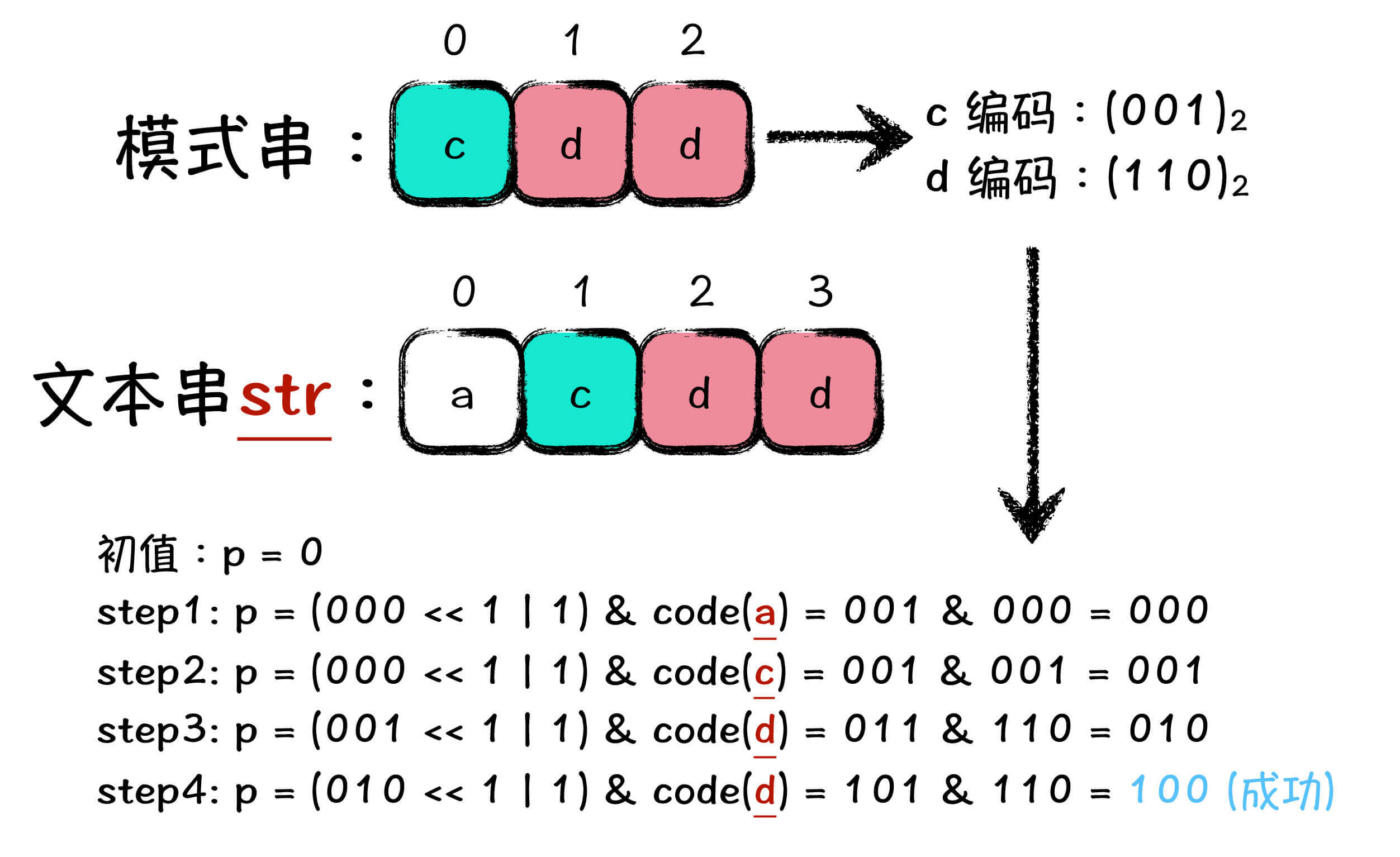
要想理解这个匹配过程,首先就是需要注意到 ,变量 p 在第四步的时候,二进制表示的第 3 位为 1 了,说明此时截止到文本串 acdd 的第 4 位为止,匹配到了原模式串 cdd。这个过程,你需要仔细琢磨琢磨,然后再往下看。
接下来我们来讨论一般情况下的 p 值,如果模式串长度为 m,那么在什么情况下,p 值的第 m 位为 1 呢?
由算法中的 p 值计算公式可知,p 是由“按位与”操作得到的值,也就是说,其中一部分 code(str[i]) 的二进制的第 m 位必须为 1,这就意味着 str[i] 是模式串第 m 位的字符。并且为了p 值的第m位为1,按位与的另一边 (p << 1 | 1) 这个值的第 m 位也必须是 1。
关于 (p << 1 | 1) 这一部分中,或 1 操作,只能影响二进制的最低位,我们可以暂时忽略它。关键就是理解 p << 1 这个操作,左移以后的第 m 位为1,说明左移之前,p 的二进制表示的 m - 1 位也是 1。
通过分析上一轮 p 的二进制表示的 m - 1 位为什么是 1 时,你会推理得到 str[i - 1] 必须是模式串 m - 1 位的字符。依次类推,你就会得到一个结论:文本串 str 的第 i - m 位,到第 i 位之间的字符串,其实就等于原模式串的内容。下面给你准备了一个示意图:
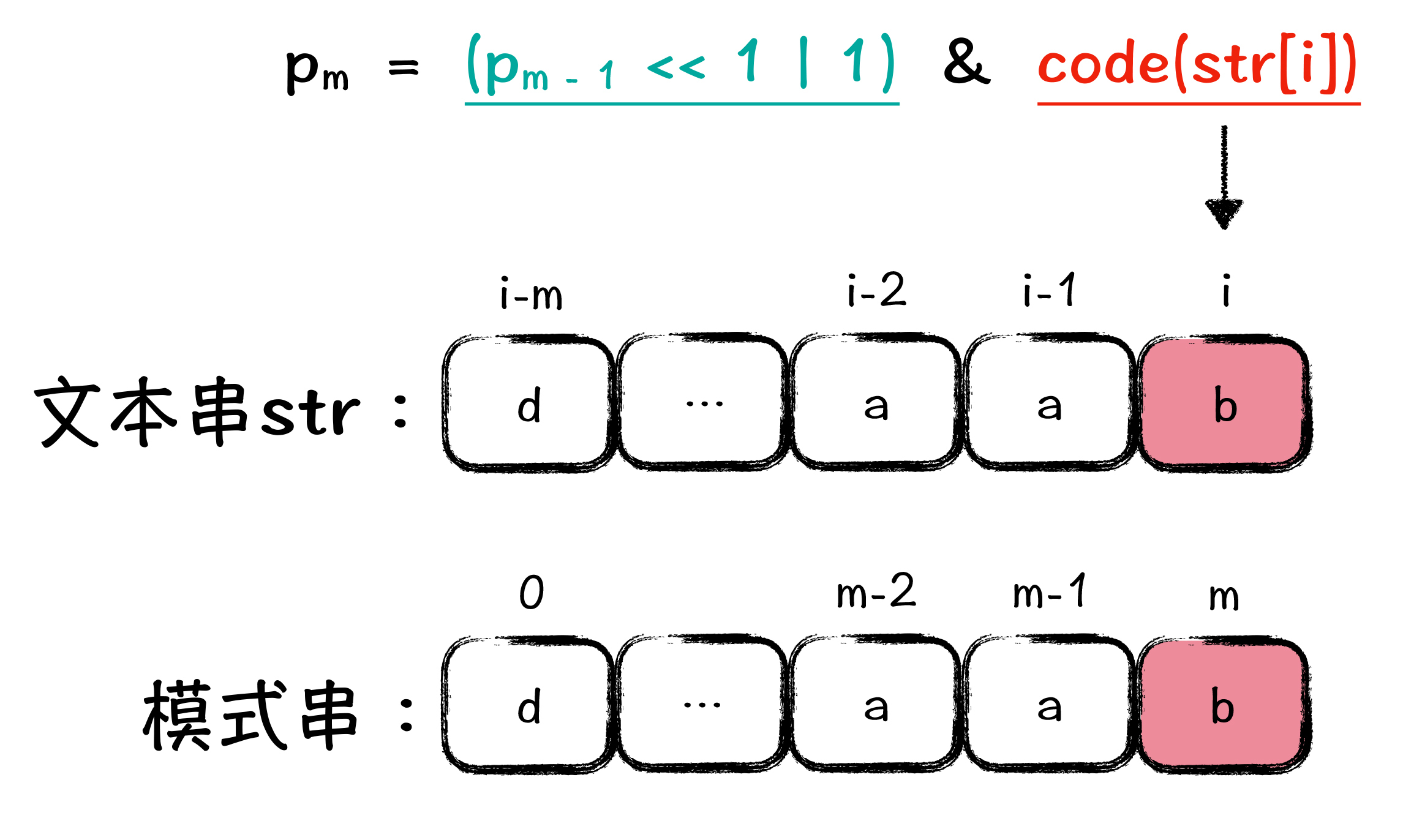
其中 $p_m$ 代表 p 的二进制表示的第 m 位为 1,$p_{m-1}$ 表示 p 的二进制表示的第 m-1 位为 1。因为只有第 m-1 位为 1,才可能左移 1 位以后的结果第 m 位为 1。
最后我们来解释一下,为什么 p 左移 1 位以后,还需要或上一个 1 。其实也很好理解,如果 str[i] 是模式串的第 0 位字符,那么 p 在什么情况下,第 0 位是 1 ?你会发现,根据之前推理,只有在上一个状态 p 的 -1 位为 1 的时候,左移以后第 0 位才可能是 1。
但我们知道,根本没有 -1 位这个位置,也就是说,如果不看或 1 操作的话,一个初值为 0 的 p 变量,想通过单纯的左移操作,第 0 位永远不可能是 1。所以这个或 1 操作,其实就是为了使得 p 左移以后的第 0 位永远置为 1,而最终计算结果中的第 0 位是否为 1,这个要看 str[i] 这个字符是否在模式串的第 0 位出现过。
关于 Shift-And 算法这个知识点呢,我大致解释完了。你在学习这块知识的时候,可能感觉有点难,没准读完第一遍的时候,脑子都是懵的。但请相信我,也相信你自己,把这几段内容多看几遍,遇到不理解的句子,停下来多思考思考,看的次数多了,你就明白是什么意思了。
至此呢,我们就学习完了 Shift-And 算法的两个重要的过程。代码实现呢,如下所示:
int shift_and(const char *str, const char *p_str) {
int code[256] = {0}, m = 0;
// 初始化每一个字符的编码
for (int i = 0; p_str[i]; i++, m++) {
code[p_str[i]] |= (1 << i);
}
int p = 0;
for (int i = 0; str[i]; i++) {
p = (p << 1 | 1) & code[str[i]];
// 如果 p 所对应的模式串最高位为1,代表匹配成功
if (p & (1 << (m - 1))) return 1;
}
return 0;
}
在这份代码中,你会发现我们只用了两次循环,注意!是两次循环,而不是两层循环。一次循环是遍历模式串,生成编码 code 信息,第二次循环是遍历文本串 str,循环迭代得到 p 变量的值,直到 p 变量的第 m 位为 1 时,就代表匹配成功。
可以看到,这种算法的时间复杂度,和暴力匹配算法比起来,提升的不是一星半点。暴力算法是 O(nm) 的,而 Shift-And 算法的时间复杂度就是 O(n + m) 的。也就意味着,同样是文本串 10000 的长度,模式串 1000 长度,Shift-And 算法,是暴力匹配算法效率的 1000 倍!
改进 Shift-And 算法
说是 1000 倍,细心的你可能会发现一个问题,上述算法中的 p 变量,是一个整型变量,也就是说,p 变量最多支持,模式串长度不超过 32 位的单模匹配问题。
请你想想,这个问题究竟是出在算法上,还是出在数据结构上?答案很显然,是出在数据结构上。要是有一种数据结构,支持很大的二进制整数表示,同时在这种结构的数据上,还可以操作左移、或运算以及按位与运算的话,这种结构就可以取代原有整型 p 变量的作用。这样,我们就可以支持长度更长的模式串的匹配问题了!
所以今天给你留的作业呢,就是请你在尽量不修改算法流程的情况下,增加一个类型结构,实现可以处理 1000 位模式串的 Shift-And 算法。欢迎你把自己的答案写在留言区,我们一起来讨论实现方法。
课程小结
通过今天这堂课呢,我希望你彻底体会到,算法和数据结构是程序设计的两个部分,并且它们可以单独来进行学习、设计和实现。
如果说,今天想让你记住点儿什么的话,那就是:等价信息表示对于解决问题很重要。这个事情不只是对于程序设计而言,很多事情都是这样。同等的信息,不同的表示形式,其实就是不同的观察角度,最终的效果也会截然不同。就像今天的 Shift-And 算法,对于模式串的信息,做了一个等价转换以后,整个算法的时间复杂度就被优化了一个数量级,这个过程值得你花时间去仔细体会。
本节课,也是我们整个“编码能力训练篇”的最后一节了,我希望你通过这部分知识的学习,掌握计算思维,以及程序设计的核心法门。下一章节,我不再赘述算法和数据结构的重要性,而是请你带着在“编码能力训练篇”掌握的技巧,随我进入“算法与数据结构篇”的学习吧!
好了,今天就到这里了,我是胡光,我们下章见。
精选留言
2020-02-22 10:57:38
数据结构的底层有两种想法,
1. 用数组,每个数组用0和1表示
2. 用字符串,用长度位N的01的字符串表示
但是C语言是不支持运算重载的,也就是位运算的符号是不能套用在新的数据结构,因此得要创建新的函数对应原来的位操作。
算法思想不变,但是代码形式会发生改变。
2020-04-13 23:03:45
2020-02-22 18:03:41
2020-08-07 16:54:25
1、文中的bruce_force例子和shift_and算法例子,我自己跑,都是内存溢出结果······
2、思考题,我硬着头皮做,心里知道这肯定是错的······
代码如下:
#include <stdio.h>
typedef struct BIGP{
int p[1000];
} ;
int shift_and(const char *str, const char *p_str){
int code[256] = {0}, m = 0;
for (int i = 0; p_str[i]; i++, m++){
code[p_str[i]] |= (1 << i);
}
struct BIGP PP;
int pp.p = {0};
for (int i = 0; str[i]; i++){
pp.p = (pp.p << 1| 1) & code[str[i]];
if (pp.p & (1 << (m - 1)))return 1;
}
return 0;
}
int main(){
struct BIG PP;
const char *str, *p_str;
scanf("%s %s", str, p_str);
printf("%s", shift_and(str, p_str));
return 0;
}
2020-03-23 08:49:18
2020-02-22 14:11:01
2022-10-27 16:09:46
#include <stdio.h>
#define SIZE 100
int arr[SIZE]; // 定义一个表示二进制大整数的数组
// 转化为二进制大整数表示
int *convert_to_big_int(int num)
{
// 每次都重新初始化二进制大整数数组
for (int i = 0; i < SIZE; i++)
{
arr[i] = 0;
}
int count = 0;
if (num == 0)
{
arr[0] = 0;
return arr;
}
do
{
arr[++count] = num % 2;
num = num / 2;
} while (num != 0);
arr[0] = count;
return arr;
}
// 二进制大整数左移一位
void big_int_left_move_one(int *arr)
{
if (arr[0] == 0)
{
arr[0] = 1;
arr[1] = 1;
return;
}
arr[0] += 1;
for (int i = arr[0]; i > 1; i--)
{
arr[i] = arr[i - 1];
}
arr[1] = 0;
}
// 二进制大整数或1操作
void big_int_or_one(int *arr)
{
arr[1] = 1;
if (arr[0] == 0)
{
arr[0] = 1;
}
}
// 二进制大整数进行与操作
void big_int_and(int *a, int *b)
{
int flag = 0;
for (int i = a[0]; i > 0; i--)
{
if (a[i] && b[i])
{
a[i] = 1;
// 判断是否是第一次进入,第一次进入则设置a[0]的长度
if (!flag)
{
a[0] = i;
flag = 1;
}
}
else
{
a[i] = 0;
}
}
// 判断之前是否与成功过,若没与成功过,则设置a[0]=0
if (!flag)
{
a[0] = 0;
}
}
// 进行shift_and算法匹配
int shift_and(const char *str, const char *p_str)
{
int code[256] = {0};
int m = 0;
// 初始化每一个字符的编码
for (int i = 0; p_str[i]; i++, m++)
{
code[p_str[i]] |= (1 << i);
}
int p[SIZE] = {0};
for (int i = 0; str[i]; i++)
{
// p = (p << 1 | 1) & code[str[i]];
int *stri = convert_to_big_int(code[str[i]]); // 把code[str[i]]进行二进制大整数表示
big_int_left_move_one(p); // p左移一位
big_int_or_one(p); // p或上1
big_int_and(p, stri); // p进行与运算
// 如果p所对应的模式串的最高位为1,代表匹配成功
if (p[m])
{
return 1;
}
}
return 0;
}
2021-03-27 03:26:48
2020-09-29 15:09:25
char *Int;
int high;
int size;
} BigInt;
BigInt* BigIntLeftShiftN(BigInt* pbi, int n) {
if (!pbi) return pbi;
if (!pbi->high && !pbi->Int[0]) return pbi;
if (n + pbi->high > pbi->size) {
DBG("Error happens, number bit exceed");
return NULL;
}
int moveN = pbi->high + 1;
pbi->high += n;
for (int i = pbi->high; moveN > 0; i--, moveN--) {
pbi->Int[i] = pbi->Int[i - 1];
}
for (--n; n >= 0; n--) {
pbi->Int[n] = 0;
}
return pbi;
}
BigInt* BigIntAnd(BigInt *target, const BigInt* src) {
if (!target || !src) {
return target;
}
if (!src->high && !src->Int[0]) {
target->high = 0;
target->Int[0] = 0;
return target;
}
int flag = 1;
for (int i = target->high; i >= 0; i--) {
target->Int[i] = target->Int[i] & src->Int[i];
if (flag) {
if (!target->Int[i]) {
target->high--;
} else {
flag = 0;
}
}
}
return target;
}
int BigIntShiftAnd(const char* text, const char* pat) {
if (!text || !pat || !strlen(text) || !strlen(pat) || strlen(text) < strlen(pat)) return -1;
int len = (int)strlen(pat);
BigInt** code = CodeInit(len);
if (!code) return -1;
for (int i = 0; pat[i]; i++) {
code[(int)pat[i]]->high = i;
code[(int)pat[i]]->Int[i] = 1;
}
BigInt* ret = BigIntGet(len);
if (!ret) {
CodeFree(code, len);
return -1;
}
int pos = -1;
for (int i = 0; text[i]; i++) {
ret = BigIntLeftShiftN(ret, 1);
ret->Int[0] = 1;
ret = BigIntAnd(ret, code[(int)text[i]]);
if (ret->high == len - 1 && ret->Int[ret->high] > 0) {
pos = i - len + 1;
break;
}
}
CodeFree(code, len);
return pos;
}
程序尝试这写出来了,验证好像没问题,就是感觉空间开销有点大。希望老师指点。评论空间有限,省略了初始化函数和销毁函数。