你好,我是胡光,咱们又见面了。
上两节呢,我们讲了素数筛这个算法,并且用素数筛算法演示了程序设计过程中的框架思维。其中提到了欧拉筛法,不知道勤奋的你有没有课后自己去学习一下呢?如果你学习了欧拉筛法以后,你会对我所说的框架思维有更深刻的体会。
在之前的文章中,我们介绍过算法和数据结构的作用。当时我讲到,算法的作用是做数据的计算,并且它对于编程的重要意义,不止是停留在那些叫得上来名字的具体算法上面,而是我们称之的算法思维。
算法思维的具体表现,就是我们处理得到相同信息时,所采用的不同的流程方法。这些方法呢,有好坏高低的比较,而评价的标准,主要就是从时空复杂度方面来考量。由于本专栏主要是教会你掌握编程思维,所以,即使你对时空复杂度不是很了解,也不用担心它会影响你的入门编程学习。你只需要知道,这是我们衡量算法好坏的重要指标即可。
前两篇文章呢,其实更多的就是给大家展示算法思维对于程序设计的重要性,并且,我还要在这里提醒一句,算法的底层是数学,适当的补充数学基础,对于算法的学习是有奇效的。
数据结构和算法,前者负责“表示数据”,后者负责“处理数据”。接下来,我将给你讲讲数据结构的重要性。
今日任务
表示数据到底是什么呢?为什么表示数据很重要?通过今天的 10 分钟任务,你就能明白其中的重要意义。这个任务很简单,就是请你实现一个程序,输出 2 的 1000 次方的结果是多少。
关于这个问题,你可能会意识到,C 语言中给我们提供的 int 类型,肯定是无法完成这个任务的,因为它表示不了这么大的数字。你可能想用 long long 类型来进行解决,那你这就要犯低级错误了。long long 是 64 位整型,也就是占 64 个 2 进制位,它顶多能表示 2 的 64 次方减 1 的结果,相对于 2 的 1000 次方来说,小太多了。
你可能又想到,既然 long long 表示不了,那就使用 double,不是说 double 是浮点数类型,可以表示很大很大的数字么?对,double 作为双精度浮点型,确实可以表示很大很大的数字,2 的 1000 次方这个数字,对于 double 的表示范围来说,也是不足挂齿的。
可这里面存在一个严重的问题,就是 double 是有精度损失的。什么意思呢?请耐心听我给你解释。
其实也很好理解,不管是long long 类型,还是double 类型,它们都是 64 位的信息,也就是说,它们都可以准确表示2的64次方个数量的数字。但是,即使 double 类型表示数字的范围比 long long 要大很多,可这个当中很多数字 double 是没有办法准确表示的。
至于 double 的表示精度,一般来说是有效数字 15 位,就是一个数字,由左向右,从第一个不为零的数字起,向后15位都是准确的。因此 double 类型实际上也没有办法,准确表示 2 的 1000 次方的计算结果。
那究竟应该如何来解决今天这个问题呢?带着这个疑问,让我们正式开始今天的释疑之行吧。
必知必会,查缺补漏
前面讲了这么多,我就是想让你明确一点,就是在我们所认识的 C 语言中,是没有任何一种数据类型,可以表示得下我们今天想要计算 2 的 1000 次方的结果。也就是说,基础类型表示不了我们今天所要计算的这个结果,那该怎么办呢?
还记得我讲过的关于结构体的相关知识么?当时我们使用结构体,创造了一个新的代表坐标点的数据类型。按照创造类型的思路去思考现在这个问题,也就是,如果我们能采用一种能够表示更大范围的整数的数字表示法,那今天这个问题,就可以解决了。这就是我们今天要学习的内容,它的大类名字叫做高精度表示法,更具体的叫做大整数表示法。
1.大整数表示法
为了完成今天这个任务,我们需要从数据的表示上下功夫。其实,数据的表示绝不是只有一种方法,就好像你想表达数字 1 的一半,你既可以用0.5来表示,也可以用1/2来表示。所以,今天我们想要表示很大很大的整数,其实也有很多方法,下面就看看我要给你介绍的方法吧。
首先我们先来思考一个事情,如果我想要存储一个 100 位的十进制数字,为什么现有的 int 数据类型做不到?本质上是因为这个数字的位数,超过了 int 能够表示数字的位数上限。int 能够表示的数字大小的上限,是一个以 2 开头的 10 位数字,而我们想要存储的,却是一个 100 位的数字。
看到了这个本质问题后,其实也就找到了解决问题的方向,那就是我们要创造的这种数字的表示方法,能够有足够的空间去容纳更多位数的数字。提起空间,你想到了什么?是不是我们之前讲到的数组?也就是说,我们开辟一个整型数组空间,让这个数组的每个位置存储一位数字,这样是不是就可以很轻松地存储 100 位数字了。
下面就来看看这种大整数表示法,是如何存储数字 3526 的吧:
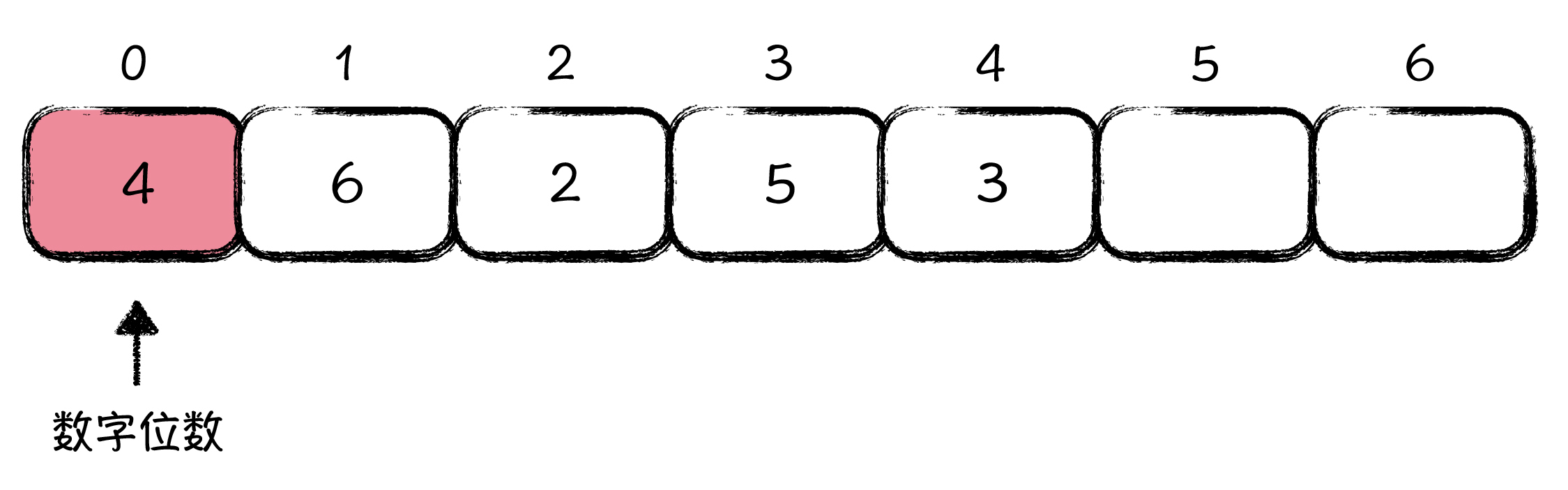
正如你所看到的,这种表示法中,使用数组的第0位存储数字的位数,因为 3526 有 4 位,所以数组的第 0 位就设置成了 4 这个值。接下来,数组从第 1 位到第 4 位记录的就是原数字 3526,可是你有没有发现,这个数字是好像是倒着放置的,数字的最高位,也放在数组的最高位中,在图上看着感觉怪怪的。
你可能会觉得别扭,可我要告诉你,这种存储方式不是无缘无故的,而是凝结了前人的智慧。最直接的一个好处,就是当你拿着两个这样的大整数做加法,产生一个新的大整数的时候,这个新产生的大整数会涉及到进位问题。
例如:95 + 12 = 107,两个两位的大整数相加,产生一个三位的大整数。在这种从右到左的倒着存储表示法中,是向着数组高位去进位,去扩充位数,这是便利可行的。可你要是从左到右去正着存储,你会发现一旦最高位产生进位,就很难处理。
2.如何计算大整数加法
你可能还是不太理解,这种大整数表示法的好处,下面我们就拿“大整数加法”来举个例子。顺便也向你展示一下,我们究竟是如何操作这种大整数。
大整数加法,顾名思义就是利用大整数表式法,做加法运算。具体怎么做,你应该还记得小学时候,老师教给我们的加法竖式吧?其实大整数加法,本质上就是参考这种竖式计算法,把每一位对齐,然后按位相加,加完以后再统一处理进位。下面,我用一张图说明大整数加法,是如何计算 445 + 9667 的:
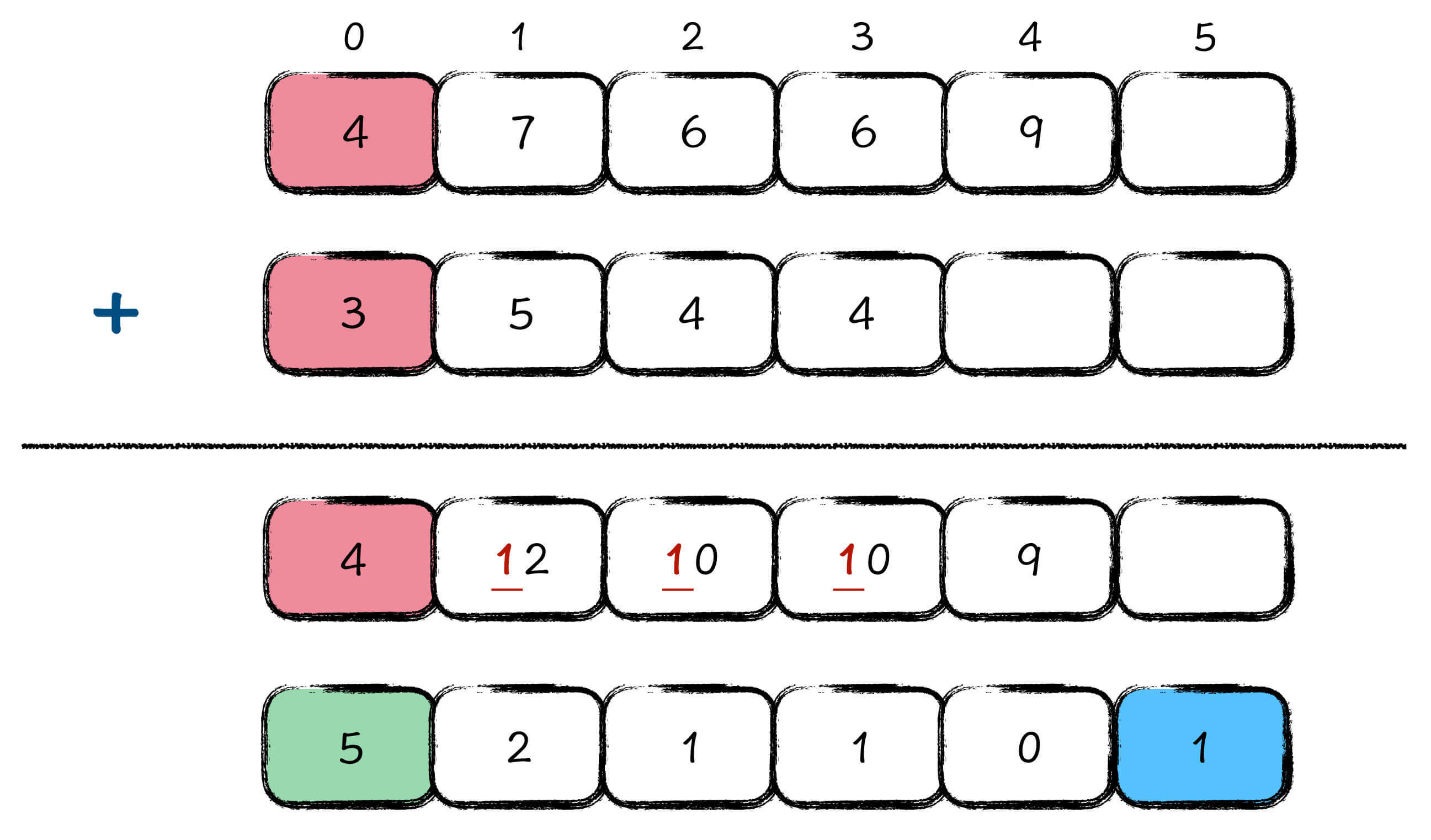
正如你所看到的,首先我们用大整数表示法,分别表示 445 和 9667 这两个数字;然后以位数最长的那个大整数,作为计算结果大整数的基础位数,445和9667按位相加,得到一个 4 位的结果大整数,4 位分别是,9、10、10、12;最后我们再依次处理进位,就得到了底下那一行的结果:10112。
在这个过程中,你会看到最高位的 9 产生了进位,最终变成了一个 5 位的大整数,产生的新最高位,我们只需要继续向后放即可。这就是我刚刚所说的,这种大整数表示法,能够非常方便地处理进位。
看完了大整数加法的过程后,不可缺少的,就是代码的实现过程。下面我给你准备了一份代码,代码中有相关注释,这是需要你自己拿出时间,来进行自学的内容。
// 定义一个交换两个变量值的宏 swap
#define swap(a, b) { \
__typeof(a) _t = a; \
a = b, b = _t; \
}
// 实现大整数加法 a + b 的结果,存放在 c 中
void plus_big_integer(int *a, int *b, int *c) {
// 让 a 指向位数较长的那个数字
if (a[0] < b[0]) swap(a, b);
// 大整数 c 的位数以 a 的位数为基准
c[0] = a[0];
// 循环模拟按位做加法
for (int i = 1; i <= a[0]; i++) {
if (i <= b[0]) c[i] = a[i] + b[i];
else c[i] = a[i];
}
// 处理每一位的进位过程
for (int i = 1; i <= c[0]; i++) {
if (c[i] < 10) continue;
// 判断是不是最高位产生了进位
// 如果是最高位产生进位,就进行初始化
if (i == c[0]) c[++c[0]] = 0;
c[i + 1] += c[i] / 10;
c[i] %= 10;
}
return ;
}
一起动手,搞事情
今天给你留的作业题,和我给你准备的那个大整数加法的代码有关。就是请你完成一个,能够实现读入两个大整数,并且输出两个大整数相加之和的程序。关于这个程序作业,你不需要考虑负数的情况,我们假设所有数字均是正整数。
这里给你个提示:在读入两个大整数的时候,你可以按照两个字符串数据进行读入,然后再把字符串数据,转换成我们上面所说的大整数表示法,最后调用上面那个大整数加法的过程。程序的关键提示已经告诉你了,剩下的部分,试试自己完成吧,加油!
突破类型,求解 ${2}^{1000}$ 的值
最后,我们回到今天的任务。
要计算 2 的 1000次方的结果,就是要计算 1000次乘法,最终的结果由于数值太大,我们肯定要使用大整数表示法了。也就是说,我们要在大整数表示法的基础上,操作 1000 次乘法,每次都是乘以 2,那么怎么做大整数乘法呢?
要想理解这个计算过程,我们还是得回到大整数表示法本身,所对应的数学模型理解上,具体请看下图:

如图所示,我们把大整数表示法中,每一个数字所对应的位权写出来,那么数组中所存储 3、5、2、6 的大整数信息,其实等价于下面的那一行数学公式,即$3 * 10^{3}+5 * 10^{2}+2 * 10^{1}+6 * 10^{0}$。
我们对3526这个大整数乘以 2,其实等价于对下面那个数学式子乘以 2,就可以得到如下结果:
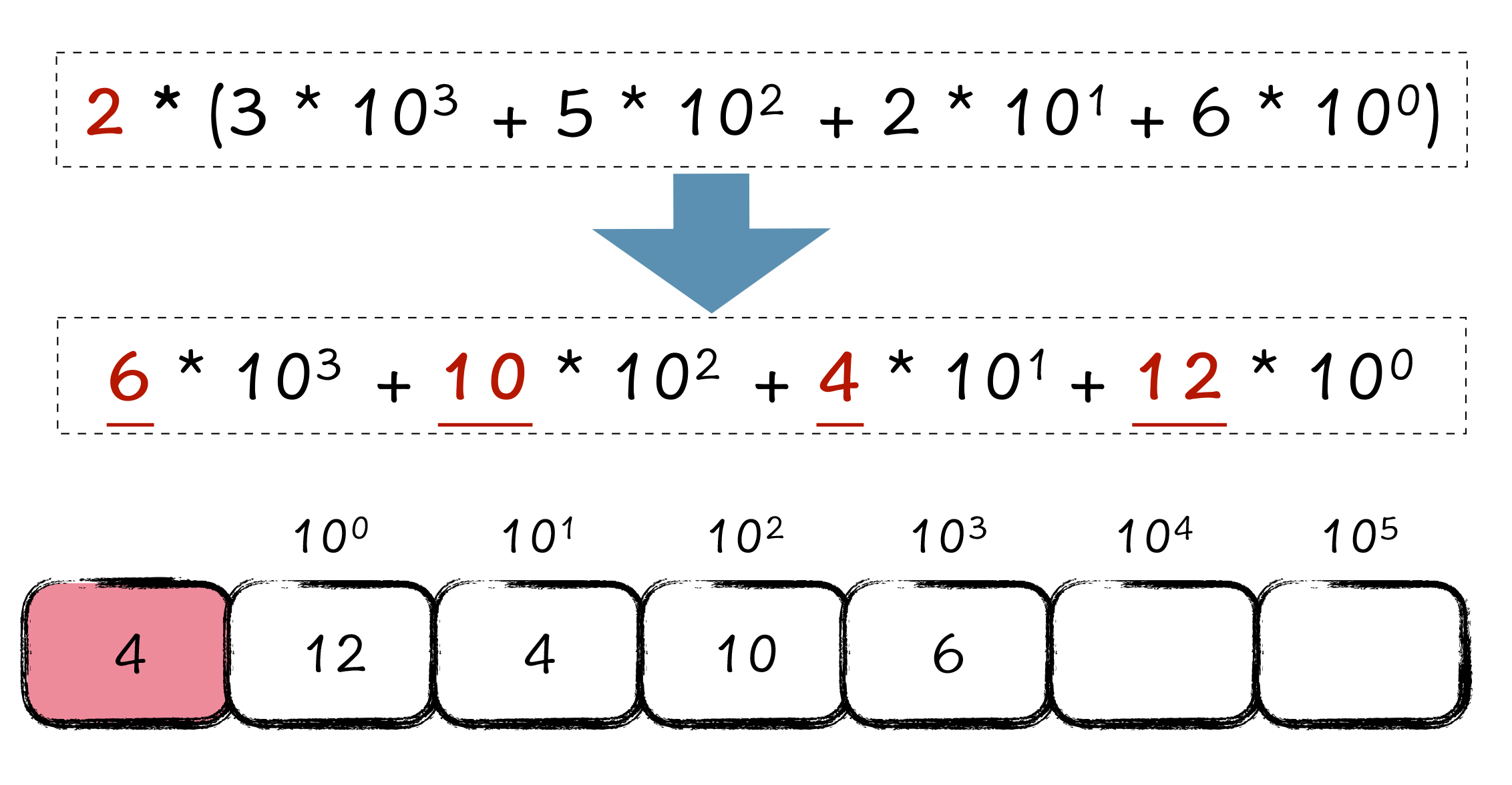
你会看到,对某个大整数乘 2 的操作,其实,可以看成是对这个大整数的每一位分别乘以 2 的操作,然后再仿照大整数加法的过程,依次处理进位即可。
最后,关于如何完成今天的任务,我给你一个参考程序。当然你也可以选择不看参考程序,自己实现这个过程。
#include <stdio.h>
// 将 num 数组初始化成大整数表示的 1
// 作用就是做累乘变量
int num[400] = {1, 1};
int main() {
// 计算 100 次 2 的 10 次方相乘的结果
for (int i = 0; i < 100; i++) {
// 对大整数的每一位乘以 2 的 10 次方
for (int j = 1; j <= num[0]; j++) num[j] *= 1024;
// 处理进位
for (int j = 1; j <= num[0]; j++) {
if (num[j] < 10) continue;
if (j == num[0]) num[++num[0]] = 0;
num[j + 1] += num[j] / 10;
num[j] %= 10;
}
}
// 输出大整数
// 由于大整数是倒着存的,所以输出的时候倒着遍历
for (int i = num[0]; i >= 1; --i) printf("%d", num[i]);
printf("\n");
return 0;
}
课程小结
解决了这个任务后,恭喜你,又变强了一点点。今天我们学习了大整数的表示法,以及大整数加法和乘法的基本操作,我希望你记住以下几点:
- 在大整数的表示法中,数字是从右到左,倒着存放在数组中的。
- 大整数的表示法,体现的是数据结构对于程序设计的作用。
- 大整数的加法和乘法过程,体现的则是算法对于程序设计的作用。
同时,你还可以看到,我们在理解大整数乘法的过程中,是从数组的表示法与数学公式的等价性这个角度出发讨论的。其实我就是想再次跟你强调那句话,就是算法的底层是数学。
而通过今天的学习,想必你已经对“数据结构本质是用作数据的表示”这句话,已经有所感觉了。综合“算法是做数据的计算”这句话,说明算法和数据结构是程序中可以独立进行设计的两个部分,关于这点呢,将是下一节咱们讲解的重点。
好了,今天就到这里了,我是胡光,我们下期见。
精选留言
2020-08-02 00:33:23
利用老师留下的模块,我多跨了几步
1、课文2的1000次方程序的完全体,计算任何正整数的正整数幂。代码如下:
/*大数幂*/
#include <stdio.h>
#include <string.h>
void print_Big(int x, int n){
int a[100000] = {1,1};
for(int i = 1; i <= n; i++){
for(int j = 1; j <= a[0]; j++)a[j] *= x;
for(int j = 1; j <= a[0]; j++){
if(a[j] < 10)continue;
if(j == a[0])a[++a[0]] = 0;
a[j + 1] += a[j] / 10;
a[j] %= 10;
}
}
for(int i = a[0]; i >= 1; --i)printf("%d", a[i]);
printf("\n");
}
int main(){
int x, n;
scanf("%d %d", &x, &n);
print_Big(x, n);
return 0;
}
其中数组a的位数不能再大了,不然就是内存溢出······
2、大数阶乘,就是计算输入的任意正整数的阶乘。代码如下:
/*大数阶乘*/
#include <stdio.h>
#include <string.h>
void print_factorial(int n){//阶乘的函数
if(n < 0){
printf("error\n");//检查机制
return;
}
else if(n == 0){
printf("1" );
return;
}
int a[100000] = {1,1};
for(int i = 2; i <= n; i++){
for(int j = 1; j <= a[0]; j++)a[j] *= i;//乘积的值
for(int j = 1; j <= a[0]; j++){
if(a[j] < 10)continue;
if( j == a[0])a[++a[0]] = 0;
a[j + 1] += a[j] /10;
a[j] %= 10;
}
}
for(int i = a[0]; i >= 1; --i)printf("%d", a[i]);//输出结果
}
int main(){
int n;
scanf("%d", &n);//输入几的阶乘
print_factorial(n);
return 0;
}
2020-07-26 17:05:04
1、课文的例子代码是在的太漂亮了
2、课文的“搞事情”,看似很简单,老师也十分亲切地给出了思路,其中的关键就是读入字符串数字,然后处理成整数数组······我找到的方法就是利用字符ACSII码性质来实现,说起来没什么,但就是整整耗了两个星期·······
3、无心插柳,我居然把老师的大数数组加法给模块化了。明明在第一次尝试改造时各种出错······
/*交作业:*/
#include <stdio.h>
#include <string.h>
void printBIG(char a[], char b[]){//定义函数printBIG,实现输入两个“字符串”大数,相加,输出“数字”大数
int c[1000] = {1,1};
int len_a, len_b;
len_a = strlen(a) ;
len_b = strlen(b) ;
c[0] = ((len_a > len_b) ? len_a : len_b);
for(int i = 1; i <= c[0]; i++){//从最小位开始相加,从左往右地放在数组C里
c[i] = (a[len_a - i] - '0') + (b[len_b - i] - '0') ;//这里字符数字换成数字数字的窍门是,字符0-9的ACSII码-48(字符0的ACSII码)=数字0-9
}
for(int i = 1; i <= c[0]; i++){//进位处理
if(c[i] < 10)continue;// 每一位是否满10?
if(i == c[0])c[++c[0]] = 0;//是否要进位
c[i + 1] += c[i] / 10;//满10进1
c[i] %= 10;//原位除10求余
}
for(int i = c[0]; i >= 1; --i)printf("%d", c[i]);//胡老师给的倒序输出语句太漂亮了,我直接拿来用了
printf("\n");
}
int main(){
char a[1000], b[1000];
scanf("%s %s", a, b);
printBIG(a, b);
return 0;
}
2020-07-30 15:12:58
之前发的代码后来发现有BUG,只要两个数的位数不一致的时候就不能正常运算。
现在修整了该BUG。
其中思路是把两个数的位数情况都遍历:相同、第一个数比第二个数多、第一个数比第二个数少。
以下是修整后的代码:
#include <stdio.h>
#include <string.h>
void printBIG(char a[], char b[]){//定义函数printBIG,实现输入两个“字符串”大数,相加,输出“数字”大数
int c[1000] = {1,1};
int len_a, len_b;
len_a = strlen(a) ;
len_b = strlen(b) ;
c[0] = ((len_a > len_b) ? len_a : len_b);
for(int i = 1; i <= c[0]; i++){//从最小位开始相加,从左往右地放在数组C里
if((len_a - i) >= 0 && (len_b - i) >= 0)//位数相同的情况
c[i] = (a[len_a - i] - '0') + (b[len_b - i] - '0') ;//这里字符数字换成数字数字的窍门是,字符0-9的ACSII码-48(字符0的ACSII码)=数字0-9
else if((len_a - i) >= 0 && (len_b - i) < 0)//数1的位数比数2大的情况
c[i] = (a[len_a - i] - '0');
else if((len_a - i) < 0 && (len_b - i) >= 0)//数1的位数比数2小的情况
c[i] = (b[len_b - i] - '0');
}
for(int i = 1; i <= c[0]; i++){//进位处理
if(c[i] < 10)continue;// 每一位是否满10?
if(i == c[0])c[++c[0]] = 0;//是否要进位
c[i + 1] += c[i] / 10;//满10进1
c[i] %= 10;//原位除10求余
}
for(int i = c[0]; i >= 1; --i)printf("%d", c[i]);//胡老师给的倒序输出语句太漂亮了,我直接拿来用了
printf("\n");
}
int main(){
char a[1000], b[1000];
scanf("%s %s", a, b);
printBIG(a, b);
return 0;
}
2020-03-01 10:14:27
2020-02-22 10:44:29
那么,有没有通过二进制本身,比如说在底层搞一个新的类型,比如说super long, 用128位或者更多位来表示这个大数据类型的方式呢?
2020-02-20 18:57:58
1,在标准C中是 以“__”开头,所以在标准C中要写成“__typeof()”或“__typeof__()”,在GNU C 中还支持直接写“typeof()”,我看您写的都是”__typeof()",其实三个都是一样的,但是否为了不造成不必要的麻烦,才用了标准C的第一个呢?
2,“一起动手搞事情”前面的代码,第23行,“c[i + 1] += c[i] / 10;”,请问这里直接用“+= 1”不行吗?我在这里看了好久才看明白就是一个“进一”的意思(笑哭)。
3,第22行,"c[++c[0]]",这里是不是让“c[0]“先加一再拿来用?用"c[0]++"就会先用原来未加一的数值,然后才加一?我理解的对吗?
谢谢老师,欧拉筛法我看了一些blog,看的头晕,不知道他们的一些变量的作用是什么?例如(https://blog.csdn.net/tianwei0822/article/details/78309453),cnt 是用来干什么的?里面的for循环看不太懂哈哈哈~
2022-10-20 18:14:17
#include <stdio.h>
#include <string.h>
// 定义交换两个变量值的宏
#define swap(a, b) \
{ \
__typeof(a) _t = a; \
a = b; \
b = _t; \
}
// 实现大整数加法,a + b的结果,存放在c中
void plus_big_integer(int *a, int *b, int *c)
{
// 让a指向位数较长的那个数
if (a[0] < b[0])
{
swap(a, b);
}
// 大整数c的位数以a的位数为基准
c[0] = a[0];
// 循环模拟按位加法
for (int i = 1; i <= a[0]; i++)
{
if (i <= b[0])
{
c[i] = a[i] + b[i];
}
else
{
c[i] = a[i];
}
}
// 处理每一位的进位过程
for (int i = 1; i <= c[0]; i++)
{
if (c[i] < 10)
{
continue;
}
// 判断是不是最高位产生了进位,如果是则进行初始化
if (i == c[0])
{
c[++c[0]] = 0;
}
c[i + 1] += c[i] / 10;
c[i] %= 10;
}
}
// 将一个数字字符串转换位大整数表示法
void trans_big_int_expression(char *str, int *arr)
{
int slen = strlen(str);
arr[0] = slen;
for (int i = 0; i < slen; i++)
{
arr[slen - i] = str[i] - 48;
}
}
void main()
{
int a[20], b[20], c[20] = {0};
char stra[20], strb[20];
scanf("%s%s", stra, strb);
// 转换为大整数表示法
trans_big_int_expression(stra, a);
trans_big_int_expression(strb, b);
// 进行大整数相加,并存入c中
plus_big_integer(a, b, c);
for (int i = 0; i < 20; i++)
{
printf("%d", c[i]);
}
}
2020-10-04 22:25:50
if (j == num[0]) num[++num[0]] = 0;
赋值为0的操作是不是可以省略,num数组在声明的时候已经初始元素全为0,还是说在有的情况下不是0,为了安全起见这样做的。
2020-04-12 20:36:54
2020-03-04 20:20:23